题目内容
圆（x-1）2+（y+3）2=2的圆心和半径分别为（ ）
| A、（-1，3），2 | ||
B、（1，-3），
| ||
| C、（1，-3），2 | ||
D、（-1，3），
|
考点：圆的标准方程
专题：直线与圆
分析：利用圆的标准方程的性质直接求解．
解答：
解：∵圆（x-1）2+（y+3）2=2，
∴圆心为（1，-3），
半径为r=
．
故选：B．
∴圆心为（1，-3），
半径为r=
| 2 |
故选：B．
点评：本题考查圆的圆心坐标和圆半径的求法，是基础题，解题时要认真审题，注意圆的标准方程的性质的灵活运用．
练习册系列答案
相关题目
设{an}是公比为正数的等比数列，若a3=4，a7=64，则a8=（ ）
| A、255 | B、256 |
| C、127 | D、128 |
在复平面内，复数
的共轭复数对应的点在第（ ）象限．
| i |
| 1+i |
| A、一 | B、二 | C、三 | D、四 |
已知集合A={x|3x≤81}，B=（-∞，a），若A∪B=B，则实数a的取值范围是（ ）
| A、[4，+∞） |
| B、（0，4] |
| C、（4，+∞） |
| D、（2，+∞） |
若两个非零向量
，
满足|
+
|=|
-
|=2|
|，则向量
+
与
-
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
如果复数z=2-ai满足条件|z-1|＜2，那么实数a的取值范围为（ ）
A、（-2
| ||||
| B、（-2，2） | ||||
| C、（-1，1） | ||||
D、（-
|
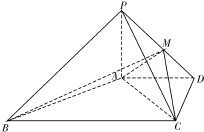如图四棱锥P-ABCD中，PA⊥平面ABCD，AD∥BC，ADCD，且AD=CD=2