题目内容
已知cosα=
，cosβ=
，且α，β∈（0，
），则cos（α-β）=（ ）
| 1 |
| 3 |
| 7 |
| 9 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
考点：两角和与差的余弦函数
专题：三角函数的求值
分析：由条件求得sinα=
，sinβ=
，再根据cos（α-β）=cosαcosβ+sinαsinβ，计算求得结果．
2
| ||
| 3 |
4
| ||
| 9 |
解答：
解：∵cosα=
，cosβ=
，且α，β∈（0，
），
∴sinα=
，sinβ=
，
∴cos（α-β）=cosαcosβ+sinαsinβ=
×
+
×
=
，
故选：B．
| 1 |
| 3 |
| 7 |
| 9 |
| π |
| 2 |
∴sinα=
2
| ||
| 3 |
4
| ||
| 9 |
∴cos（α-β）=cosαcosβ+sinαsinβ=
| 1 |
| 3 |
| 7 |
| 9 |
2
| ||
| 3 |
4
| ||
| 9 |
| 23 |
| 27 |
故选：B．
点评：本题主要考查同角三角函数的基本关系，两角差的余弦公式的应用，属于中档题．
练习册系列答案
小学同步三练核心密卷系列答案
相关题目
在复平面内，复数
的共轭复数对应的点在第（ ）象限．
| i |
| 1+i |
| A、一 | B、二 | C、三 | D、四 |
若两个非零向量
，
满足|
+
|=|
-
|=2|
|，则向量
+
与
-
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
设集合U={1，2，3，4，5}，A={1，3，5}，B={2，3，5}，则∁U（A∪B）等于（ ）
| A、{1，2，4} | B、{4} |
| C、{3，5} | D、∅ |
如果复数z=2-ai满足条件|z-1|＜2，那么实数a的取值范围为（ ）
A、（-2
| ||||
| B、（-2，2） | ||||
| C、（-1，1） | ||||
D、（-
|
下列方程所表示的曲线中，关于x轴和y轴都对称的是（ ）
| A、x2-y2=1 |
| B、y2=x |
| C、（x-1）2+y2=1 |
| D、x-y+1=0 |
由a1=1，an+1=
给出的数列{an}的第33项是（ ）
| an |
| 3an+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
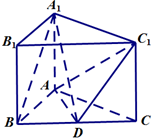如图三棱柱ABC-A1B1C1中，侧棱与底面垂直，△ABC是等边三角形，点D是BC的中点．