题目内容
7.已知首项不为0的等差数列{an}中,前n项和为Sn,满足a4=2a2,且S1,S2,S4-1成等比数列.(Ⅰ)求an和Sn;
(Ⅱ)记${b_n}=\frac{1}{S_n}$,数列{bn}的前项和Tn.若3m-8≤Tn<2m-1对任意n∈N*恒成立,求实数m的取值范围.
分析 (Ⅰ)利用等差数列的关系求得公差d,再求的通项公式an和前n项公式Sn,(Ⅱ)写出bn写出的通项公式,利用裂项法求得前n项公式Sn,再利用函数的单调性,建立方程组,求得m的取值范围.
解答 (Ⅰ)设公差为d,
则$\left\{\begin{array}{l}{a_4}=2{a_2}\\{S_1}•({S_4}-1)=S_2^2\end{array}\right.$即$\left\{\begin{array}{l}{a_1}+3d=2({a_1}+d),\;\;\;\;\;\;\;①\\{a_1}•(4{a_1}+6d-1)={(2{a_1}+d)^2},\;\;②\end{array}\right.$(1分)
由①得a1=d,代入②式得${a_1}•(10{a_1}-1)=9a_1^2$,
由a1≠0,得10a1-1=9a1,所以a1=d=1,(3分)
所以an=n,则${S_n}=\frac{1+n}{2}×n=\frac{1}{2}n(n+1)$.(4分)
(Ⅱ)可得${b_n}=\frac{2}{n(n+1)}=2(\frac{1}{n}-\frac{1}{n+1})$,(6分)
所以${T_n}=2(\frac{1}{1}-\frac{1}{2})+2(\frac{1}{2}-\frac{1}{3})+2(\frac{1}{3}-\frac{1}{4})+…+2(\frac{1}{n}-\frac{1}{n+1})=2(1-\frac{1}{n+1})$,(8分)
由于$2(1-\frac{1}{n+1})$为随n的增大而增大,可得,(10分)
∵3m-8≤Tn<2m-1恒成立,
∴$\left\{\begin{array}{l}{3m-8≤1}\\{2m-1≥2}\end{array}\right.$解$\frac{3}{2}≤m≤3$.
所以实数m的取值范围是$[\frac{3}{2},3]$.(12分)
点评 本题考查求等差数列的前n项和即通项公式,以及列项法求前n项和的方法,再求m的取值范围,属于中档题.

 通城学典默写能手系列答案
通城学典默写能手系列答案| A. | [9,+∞) | B. | [-$\frac{1}{3}$,+∞) | C. | [-$\frac{5}{3}$,+∞) | D. | [-$\frac{1}{3}$,9] |
| A. | (-$\frac{3}{5}$,-$\frac{4}{5}$) | B. | (0,1) | C. | (3,4) | D. | ($\frac{4}{5}$,$\frac{3}{5}$) |
| A. | (1,4) | B. | (2,4) | C. | (1,2) | D. | (1,+∞) |
| A. | p∧q | B. | p∧¬q | C. | ¬p∧q | D. | ¬p∧¬q |
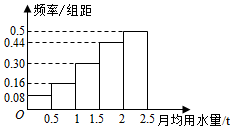 如图为某小区100为居民2015年月平均用水量(单位:t)的频率分布直方图的一部分,据此可求这100位居民月平均用水量的中位数为2.02吨.
如图为某小区100为居民2015年月平均用水量(单位:t)的频率分布直方图的一部分,据此可求这100位居民月平均用水量的中位数为2.02吨. 函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\frac{{\sqrt{6}}}{2}$.
函数f(x)=Asin(ωx+φ)(A>0,ω>0)的部分图象如图所示,则f(0)=$\frac{{\sqrt{6}}}{2}$.