题目内容

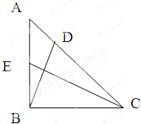等腰直角三角形ABC中，AB=BC=2，
CD
=2
DA
．
（1）求|
BD
|；
（2）线段AB上是否存在点E，使得CE⊥BD？若不存在，说明理由；若存在，指出E点的位置．
考点：向量在几何中的应用
专题：平面向量及应用
分析：（1）|
BD
|=
(
BC
+
CD
)2
利用向量的运算法则即可求得；
（2）假设存在
BE
=t
BA
时，使得CE⊥BD，则
CE
•
BD
=0，即（
BE
-
BC
）（
BC
+
CD
）=0，进行向量运算即可求得t．
解答： 解：（1）∵AB=BC=2，
CD
=2
DA
．
∴
|CD
|=
2
3
|CA
|=
4
2
3

∴|
BD
|=
(
BC
+
CD
)2
=
|
BC
|2+2|
BC
||
CD
|cos
π
4
+|
CD
|2
=
22+2×2×
4
2
3
×
2
2
+(
4
2
3
)2
=
2
29
3
．
（2）假设当
BE
=t
BA
时，使得CE⊥BD，
∵
CE
=
BE
-
BC
，
BD
=
BC
+
CD
，
∴
CE
•
BD
=0，即（
BE
-
BC
）（
BC
+
CD
）=0，
BE
•
BC
+
BE
•
CD
-
BC
2-
BC
•
CD
=0
2t×
2
2
-4-2×
4
2
3
×（-
2
2
）=0，
解得t=
2
2
3
．
E点满足
BE
=
2
2
3
BA
时，使得CE⊥BD．
点评：本题主要考查向量的运算知识，解题时注意向量的夹角别弄错了．
练习册系列答案
相关题目
若不等式ax2+abx+b≤0的解集为[-1，3]，则a+b=
 
．
已知F1、F2分别为椭圆
x2
a2
+
y2
b2
=1﹙a＞b＞0﹚的左、右焦点，M、N分别为其左右顶点，过F2的直线L与椭圆相交于A、B两点，当直线L与x轴垂直时，四边形AMBN的面积等于
 
．
已知椭圆C：
x2 
a2
+
y2
b2
═1的左右焦点为F1，F2，e=
1
3
过F1的直线l交椭圆C于A、B两点，|AF2||AB||BF2|成等差数列，|AB|=4．
（1）求椭圆C的方程．
（2）M、N是椭圆C上的两点，若MN被直线x=1平分，证明MN的中垂线过定点．
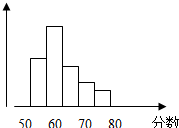某中学举行电脑知识竞赛，满分为100分，80分以上为优秀（含80分）现将高一两个班参赛学生的成绩进行整理后分成5组，绘制成频率分布直方图如图所示．已知图中从左到右的第一、三、四、五小组的频率分别为 0.30、0.15、10、0.05，而第二小组的频数是40，则参赛的人数是
 
；成绩优秀的频率是
 
．
已知向量
a
，
b
为单位向量，且
a
•
b
=-
1
2
，向量
c
与
a
+
b
共线，则|
a
+
c
|的最小值为
 
．
不等式x-4y+4≥0表示的平面区域在直线x-4y+4=0的（　　）
A、左下方及直线上的点
B、右下方及直线上的点
C、左上方及直线上的点
D、右上方及直线上的点
函数=Asin（ωx+θ）+b（A＞0，ω＞0，-π＜θ＜π）在一个周期内，当x=
π
6
时，y取最大值2，其图象与x轴的相邻两个交点的距离为
π
2
．
（1）求此函数的解析式，
（2）求函数g（x）=
1
f(x+
π
6
)
的值域．
已知0＜α＜
π
2
，求证：sinα＜α＜tanα．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网