题目内容
已知0<α<
,求证:sinα<α<tanα.
| π |
| 2 |
考点:三角函数线
专题:三角函数的求值
分析:由条件构造函数,利用导数的符号证明函数的单调性,由函数的单调性比较函数的值的大小,从而得出结论.
解答:
解:由0<α<
,可得sinα、α、tanα都是正实数.
设f(α)=α-sinα,求导得:f′(α)=1-cosα>0,
因此,f(α)=α-sinα在α∈(0,
)上是个增函数,
则有f(α)=α-sinα>f(0)=0,即sinα<α.
同理,令g(α)=tanα-α,则g′(α)=
-1>0,
所以,g(α)=tanα-α在α∈(0,
)上也是个增函数,
也有g(α)=tanα-α>g(0)=0,即tanα>α.
综上,当α∈(0,
)时,sinα<α<tanα.
| π |
| 2 |
设f(α)=α-sinα,求导得:f′(α)=1-cosα>0,
因此,f(α)=α-sinα在α∈(0,
| π |
| 2 |
则有f(α)=α-sinα>f(0)=0,即sinα<α.
同理,令g(α)=tanα-α,则g′(α)=
| 1 |
| cos2α |
所以,g(α)=tanα-α在α∈(0,
| π |
| 2 |
也有g(α)=tanα-α>g(0)=0,即tanα>α.
综上,当α∈(0,
| π |
| 2 |
点评:本题主要考查利用导数的符号证明函数的单调性,利用函数的单调性比较函数的值的大小,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
如图,正方体ABCD-A1B1C1D1中,直线AB1与BC1所成角为( )


| A、30° | B、45° |
| C、60° | D、90° |
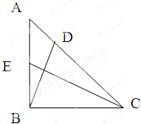 等腰直角三角形ABC中,AB=BC=2,
等腰直角三角形ABC中,AB=BC=2,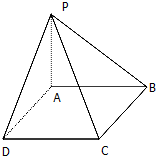 如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=
如图,四棱锥P-ABCD的底面是边长为1的正方形,PA⊥CD,PA=1,PD=