题目内容
已知变量x,y满足约束条件
,则z=x2+y2-1的最大值为( )
|
| A、12 | B、14 | C、15 | D、16 |
考点:简单线性规划
专题:数形结合
分析:由约束条件作出可行域,数形结合得到最优解,联立方程组求出最优解的坐标,代入z=x2+y2-1求其最大值.
解答:
解:由约束条件
作出可行域如图,

联立
,解得
,
∴B(3,2),
则可行域内的动点到原点的距离的最大值的平方为x2+y2=32+22=13.
∴z=x2+y2-1的最大值为14.
故选:B.
|

联立
|
|
∴B(3,2),
则可行域内的动点到原点的距离的最大值的平方为x2+y2=32+22=13.
∴z=x2+y2-1的最大值为14.
故选:B.
点评:本题考查了简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
如图,在矩形ABCD中,AB=2,BC=
,E是CD的中点,那么
•
=( )
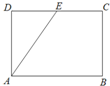
| 3 |
| AE |
| DC |

| A、4 | ||
| B、2 | ||
C、
| ||
| D、1 |
已知平面a⊥平面β,a∩β=l,点A∈a,A∉l,直线AB∥β,直线AC⊥l,直线AD⊥β,则下列四种位置关系中,不一定成立的是( )
| A、AB∥l | B、AC⊥AB |
| C、AD与l相交 | D、AC⊥β |
已知函数f(x)是定义在R上的奇函数,当x∈(-∞,0)时,有xf′(x)<f(-x)成立.(其中f′(x)是f(x)的导函数),若a=
f(
),b=f(1),c=log2
f(log2
)则a,b,c的大小关系是( )
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 4 |
| A、a>b>c |
| B、c>b>a |
| C、b>a>c |
| D、c>a>b |
从数字1,2,3,4,5中,任意取出两个数字,不是连续的自然数的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
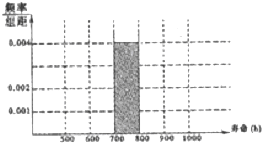 对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表:
对400个某种型号的电子元件进行寿命追踪调查,其频率分布表如表: