题目内容
已知平面a⊥平面β,a∩β=l,点A∈a,A∉l,直线AB∥β,直线AC⊥l,直线AD⊥β,则下列四种位置关系中,不一定成立的是( )
| A、AB∥l | B、AC⊥AB |
| C、AD与l相交 | D、AC⊥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:利用空间中线线、线面、面面垂直的性质求解.
解答:
解:∵平面a⊥平面β,a∩β=l,点A∈a,A∉l,
直线AB∥β,直线AC⊥l,直线AD⊥β,
∴C与D重合,AB与l平行或异面,故A错误;
∵AC⊥β,AB∥β,∴AC⊥AB,故B正确.
∵AD⊥β,∴AD与l相交,故C正确;
∵AC⊥l,平面a⊥平面β,a∩β=l,∴AC⊥β,故D正确.
故选:A.
直线AB∥β,直线AC⊥l,直线AD⊥β,
∴C与D重合,AB与l平行或异面,故A错误;
∵AC⊥β,AB∥β,∴AC⊥AB,故B正确.
∵AD⊥β,∴AD与l相交,故C正确;
∵AC⊥l,平面a⊥平面β,a∩β=l,∴AC⊥β,故D正确.
故选:A.
点评:本题考查命题真假的判断,是基础题,解题时要注意空间思维能力的培养.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
已知{an}是公差不为0的等差数列,{bn}是等比数列,其中a1=b1=1,a4=7,a5=b2,且存在常数a,β使得对每一个正数n都有an=1ogabn+β,则a+β=( )
| A、2 | B、4 | C、6 | D、8 |
已知变量x,y满足约束条件
,则z=x2+y2-1的最大值为( )
|
| A、12 | B、14 | C、15 | D、16 |
某几何体的三视图如图所示,则该几何体的表面积( )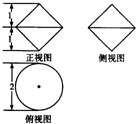

A、
| ||
B、2
| ||
C、(2
| ||
D、(2
|
三角形的三边均为整数,且最长的边为11,则这样的三角形的个数有( )个.
| A、25 | B、26 | C、32 | D、36 |
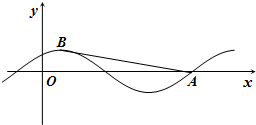 已知函数f(x)=2
已知函数f(x)=2