题目内容
圆C:x2+y2+2x-3=0和直线l:3x+4y+8=0交与A,B不同的两点,则三角形△ABC(C为圆心)的面积为( )
| A、1 | ||
B、2
| ||
C、
| ||
| D、4 |
考点:直线与圆相交的性质
专题:直线与圆
分析:三角形△ABC(C为圆心)的面积等于弦长AB乘以圆心C(-1,0)到直线l:3x+4y+8=0的距离d,由此能求出结果.
解答:
解:圆C:x2+y2+2x-3=0的圆心C(-1,0),半径r=
=2,
圆心C(-1,0)到直线l:3x+4y+8=0的距离d=
=1,
∴|AB|=2
=2
,
∴△ABC的面积S△ABC=
|AB|•d=
×2
×1=
.
故选:C.
| 1 |
| 2 |
| 22+4×3 |
圆心C(-1,0)到直线l:3x+4y+8=0的距离d=
| |-3+0+8| | ||
|
∴|AB|=2
| 22-12 |
| 3 |
∴△ABC的面积S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
故选:C.
点评:本题考查三角形面积的求法,是基础题,解题时要注意弦长的求法,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
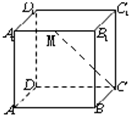 如图,在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则MC与平面ABCD所成角的正弦值等于( )
如图,在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则MC与平面ABCD所成角的正弦值等于( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在约束条件
下,目标函数z=ax+by(a>0,b>0)的最大值为
,则ab的最大值为( )
|
| 1 |
| 4 |
| A、32 | ||
| B、64 | ||
C、
| ||
D、
|
甲同学参加一次英语口语考试,已知在备选的10道题中,甲能答对其中的5道题,规定每次考试都从备选题中随机抽出3题进行测试,至少答对2道题才算合格.则甲合格的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
若tanα=
,则
的值为( )
| 1 |
| 3 |
| sinα+cosα |
| sinα-cosα |
| A、1 | B、-1 | C、2 | D、-2 |
总周长为12m的钢条制作一个长方体容器的框架,如果所制作容器的底面的相邻两边长之比为1:2,那么容器容积最大时,长方体的高为( )
| A、2m | B、1m |
| C、1.6m | D、3m |
已知等差数列{an}的前n项和为Sn,且S3=6,则5a1+a7的值为( )
| A、12 | B、10 | C、24 | D、6 |