题目内容
已知函数f(x)=|x-2a|+|x-a|,a∈R,a≠0.
(Ⅰ)当a=1时,解不等式:f(x)>2;
(Ⅱ)若b∈R且B≠0,证明:f(b)≥f(a),并说明等号成立时满足的条件.
(Ⅰ)当a=1时,解不等式:f(x)>2;
(Ⅱ)若b∈R且B≠0,证明:f(b)≥f(a),并说明等号成立时满足的条件.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:(1)将a=1代入,不等式化为具体的绝对值不等式,然后讨论解之;
(Ⅱ)由题知f(a)=|a|,f(b)=|b-2a|+|b-a|=|2a-b|+|b-a|≥|2a-b+b-a|=|a|,得证.
(Ⅱ)由题知f(a)=|a|,f(b)=|b-2a|+|b-a|=|2a-b|+|b-a|≥|2a-b+b-a|=|a|,得证.
解答:
解:(Ⅰ)因为a=1,所以原不等式f(x)>2为|x-2|+|x-1|>2.
当x≤1时,原不等式化简为1-2x>0,即x<
;当1<x≤2时,原不等式化简为1>2,即x∈∅;
当x>2时,原不等式化简为2x-3>2,即x>
.
综上,原不等式的解集为{x|x<
或x>
}.…(5分)
(Ⅱ)由题知f(a)=|a|,
f(b)=|b-2a|+|b-a|=|2a-b|+|b-a|≥|2a-b+b-a|=|a|,
所以f(b)≥f(a),(8分)
又等号成立当且仅当2a-b与b-a同号或它们至少有一个为零.…(10分)
当x≤1时,原不等式化简为1-2x>0,即x<
| 1 |
| 2 |
当x>2时,原不等式化简为2x-3>2,即x>
| 5 |
| 2 |
综上,原不等式的解集为{x|x<
| 1 |
| 2 |
| 5 |
| 2 |
(Ⅱ)由题知f(a)=|a|,
f(b)=|b-2a|+|b-a|=|2a-b|+|b-a|≥|2a-b+b-a|=|a|,
所以f(b)≥f(a),(8分)
又等号成立当且仅当2a-b与b-a同号或它们至少有一个为零.…(10分)
点评:本题考查了绝对值不等式的解法;考查了讨论的数学思想.

练习册系列答案
相关题目
关于x的方程(
)|x|-a-1=0有解,则a的取值范围是( )
| 1 |
| 3 |
| A、0<a≤1 | B、-1<a≤0 |
| C、a≥1 | D、a>0 |
设抛物线y2=8x上一点P到y轴距离是6,则点p到该抛物线焦点的距离是( )
| A、12 | B、8 | C、6 | D、4 |
若2m+8n<2
,则点(m,n)必在( )
| 2 |
| A、直线x+y=1的左下方 |
| B、直线x+y=1的右上方 |
| C、直线x+3y=1的左下方 |
| D、直线x+3y=1的右上方 |
方程2a•9sinx+4a•3sinx+a-8=0有解,则a的取值范围是( )
A、
| ||||
| B、a>0 | ||||
C、0<a≤
| ||||
| D、a>0或a≤-8 |
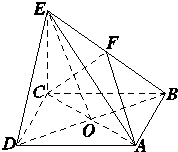 如图所示,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
如图所示,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.