题目内容
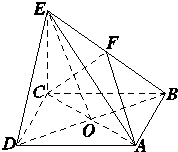 如图所示,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.
如图所示,在四棱锥E-ABCD中,底面ABCD是正方形,AC与BD交于点O,EC⊥底面ABCD,F为BE的中点.(1)求证:平面BDE⊥平面ACE;
(2)已知CE=1,点M为线段BD上的一个动点,直线EM与平面ABCD所成角的最大值为
| π |
| 4 |
①求正方形ABCD的边长;
②在线段EO上是否存在一点G,使得CG⊥平面BDE?若存在,求出
| EG |
| EO |
考点:平面与平面垂直的判定,与二面角有关的立体几何综合题
专题:空间位置关系与距离
分析:(1)证明BD⊥AC,BD⊥EC,从而证明平面BDE⊥平面ACE.
(2)由EC是平面ABCD的垂线,当M为O点时,直线EM与平面ABCD所成角的最大,从而求正方形ABCD的边长;当G为EO中点时,存在CG⊥平面BDE.
(2)由EC是平面ABCD的垂线,当M为O点时,直线EM与平面ABCD所成角的最大,从而求正方形ABCD的边长;当G为EO中点时,存在CG⊥平面BDE.
解答:
解:(1)证明:∵底面ABCD是正方形
∴BD⊥AC,
∵EC⊥底面ABCD
∴BD⊥EC
∴BD⊥平面ACE,
∴平面BDE⊥平面ACE.
(2)①点M为线段BD上的一个动点,
∵EC⊥底面ABCD
∴直线EM与平面ABCD所成角为∠EMC,tan∠EMC=
.
当CM最小时,直线EM与平面ABCD所成角的最大,
当BD⊥CM时,即M为O点时,直线EM与平面ABCD所成角的最大.
此时CO=1,正方形ABCD的边长为
.
②存在,当G为EO中点时,即
=
时,CG⊥平面BDE.
∴BD⊥平面ACE
∴BD⊥CG,
又∵△ECO为等腰三角形
∴CG⊥EO,
∴CG⊥平面BDE.
∴BD⊥AC,
∵EC⊥底面ABCD
∴BD⊥EC
∴BD⊥平面ACE,
∴平面BDE⊥平面ACE.
(2)①点M为线段BD上的一个动点,
∵EC⊥底面ABCD
∴直线EM与平面ABCD所成角为∠EMC,tan∠EMC=
| EC |
| CM |
当CM最小时,直线EM与平面ABCD所成角的最大,
当BD⊥CM时,即M为O点时,直线EM与平面ABCD所成角的最大.
此时CO=1,正方形ABCD的边长为
| 2 |
②存在,当G为EO中点时,即
| EG |
| EO |
| 1 |
| 2 |
∴BD⊥平面ACE
∴BD⊥CG,
又∵△ECO为等腰三角形
∴CG⊥EO,
∴CG⊥平面BDE.
点评:本题主要考查线面垂直、面面垂直、线面角等知识,属于中档题.

练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
执行如图所示的程序框图,输出i的值为( )


| A、2 | B、3 | C、4 | D、5 |
已知f(x)=
无极值,则b的值为( )
| 2x-b |
| (x-1)2 |
| A、1 | B、2 | C、3 | D、4 |


 在海岛A上有一座海拔
在海岛A上有一座海拔