题目内容
在区间[-3，5]上随机取一个数a，则使函数f（x）=x2+2ax+4无零点的概率是 ．
考点：几何概型
专题：概率与统计
分析：本题属于几何概型，只要求出区间长度以及满足条件的区间长度，由几何概型公式解答．
解答：
解：由已知区间[-3，5]长度为8，
使函数f（x）=x2+2ax+4无零点即判别式△=4a2-16＜0，解得-2＜a＜2，即（-2，2），区间长度为4，
由几何概型的公式得使函数f（x）=x2+2ax+4无零点的概率是
=
；
故答案为：
．
使函数f（x）=x2+2ax+4无零点即判别式△=4a2-16＜0，解得-2＜a＜2，即（-2，2），区间长度为4，
由几何概型的公式得使函数f（x）=x2+2ax+4无零点的概率是
| 4 |
| 8 |
| 1 |
| 2 |
故答案为：
| 1 |
| 2 |
点评：本题考查了几何概型的运用；关键是明确几何测度，利用公式解答．
练习册系列答案
阶梯计算系列答案
相关题目
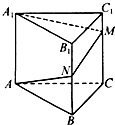已知三棱柱AB-A1B1C1的侧棱垂直于底面，且底面边长与侧棱长都等于3，蚂蚁从A点沿侧面经过棱BB1上的点N和CC1上的点M爬到点A1，如图所示，则当蚂蚁爬过的路程最短时，直线MN与平面ABC所成角的正弦值为如图为一个几何体的三视图，尺寸如图所示，则该几何体的体积为（ ）
A、2
| ||||||
B、3
| ||||||
C、5
| ||||||
D、5
|