题目内容
已知函数f（x）=
，若f（x1）=f（x2）=f（x3）（x1、x2、x3互不相等），且x1+x2+x3的取值范围为（1，8），则实数m的值为 ．
|
考点：分段函数的应用
专题：数形结合,函数的性质及应用
分析：作出函数f（x）=|2x+1|的图象，令t=f（x1）=f（x2）=f（x3），设x1＜x2＜x3，由图象的对称性可得x1+x2=-1，由条件可得2＜x3＜9．作出y=log2（x-m）（x＞1）的图象，由0＜t＜3，即可得到m的值．
解答：
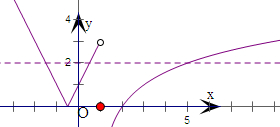解：作出函数f（x）=|2x+1|的图象，
令t=f（x1）=f（x2）=f（x3），设x1＜x2＜x3，
则有x1+x2=-1，
由x1+x2+x3的取值范围为（1，8），
则1＜-1+x3＜8，即2＜x3＜9．
作出y=log2（x-m）（x＞1）的图象，
由0＜t＜3，即有log2（2-m）=0，log2（9-m）=3，
解得m=1．
故答案为：1．
解：作出函数f（x）=|2x+1|的图象，令t=f（x1）=f（x2）=f（x3），设x1＜x2＜x3，
则有x1+x2=-1，
由x1+x2+x3的取值范围为（1，8），
则1＜-1+x3＜8，即2＜x3＜9．
作出y=log2（x-m）（x＞1）的图象，
由0＜t＜3，即有log2（2-m）=0，log2（9-m）=3，
解得m=1．
故答案为：1．
点评：本题考查分段函数的图象和运用，主要考查函数的对称性和对数的运算性质，正确画图和通过图象观察是解题的关键．
练习册系列答案
相关题目
| ∫ | 1 0 |
| 4-x2 |
A、
| ||||||
| B、π | ||||||
C、
| ||||||
D、
|
已知条件p：x2-3x-4≤0，条件q：x2-6x+9-m2≤0．若p是q的充分不必要条件，则m的取值范围是（ ）
| A、[-1，1] |
| B、[-4，4] |
| C、（-∞，-4]∪[4，+∞） |
| D、（-∞，-1]∪[4，+∞） |
如图所示的程序框图的输出结果是（ ）
| A、7 | B、8 | C、9 | D、10 |