题目内容

已知实数x，y满足
x2
4
+y2=1，求x+y的最大值．
考点：基本不等式
专题：不等式的解法及应用
分析：由条件利用三角代换、辅助角公式求得x+y=2cosθ+sinθ=
5
sin（θ+α），再利用正弦函数的值域求得x+y的最大值．
解答： 解：∵实数x，y满足
x2
4
+y2=1，∴可令x=2cosθ，y=sinθ，
∴x+y=2cosθ+sinθ=
5
（
2
5
cosθ+
1
5
sinθ）=
5
sin（θ+α），
其中，sinα=
2
5
，cosα=
1
5
，
故x+y的最大值为
5
．
点评：本题主要考查三角代换、辅助角公式的应用，正弦函数的值域，属于基础题．
练习册系列答案
相关题目
已知
3x3+4y3=7
4x4+3y4=16
，求x+y．
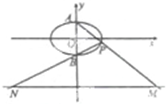如图，已知椭圆C：
x2
a2
+
y2
a2-1
=1的离心率为
2
2
，上、下顶点分别为A、B，点P在椭圆C上，且异于点A、B，直线AP、BP与直线y=-3分别相交于点M、N，设直线AP、BP的斜率分别为k1、k2．
（Ⅰ）求椭圆C的方程；
（Ⅱ）证明：k1•k2为定值；
（Ⅲ）求直线MN长度的最小值．
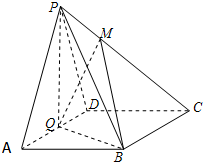如图，在四棱锥P-ABCD中，底面ABCD为菱形，∠BAD=60°，Q为AD的中点，点M在线段PC上，MC=2PM．
（Ⅰ）求证：PA∥平面MQB；
（Ⅱ）若平面PAD⊥平面ABCD，PA=PD=AD=2，求二面角M-BQ-C的大小．
已知正项数列{an}的前n项和Sn满足：Sn2-（n2+2n-3）Sn-3（n2+2n）=0（n∈N*）
（Ⅰ）求证：Sn=n2+2n；
（Ⅱ）求数列{
1
Sn
}的前n项和Tn．
已知直线l的参数方程：
x=1+tcosθ
y=tsinθ
（t为参数），曲线C的参数方程：
x=
2
cosα
y=sinα
（α为参数），且直线交曲线C于A，B两点．
（Ⅰ）将曲线C的参数方程化为普通方程，并求θ=
π
4
时，|AB|的长度；
（Ⅱ）已知点P：（1，0），求当直线倾斜角θ变化时，|PA|•|PB|的范围．
在平面直角坐标系xOy中，设动点P，Q都在曲线C：
x=1+2cosθ 
y=2sinθ
（θ为参数）上，且这两点对应的参数分别为θ=α与θ=2α（0＜α＜2π），设PQ的中点M与定点A（1，0）间的距离为d，求d的取值范围．
如果函数y=
2kx+1
kx2+4kx+3
的定义域为R，则实数k的取值范围
 
．
若关于x的不等式|x|＞ax的解集为{x|x＞0}，则a的取值范围是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网