题目内容
 如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=
如图,四棱锥S-ABCD中,ABCD为矩形,SD⊥AD,且SD⊥AB,AD=a(a>0),AB=2AD,SD=| 3 |
(1)求证:AE⊥平面SBD;
(2)求二面角A-SB-D的余弦值.
考点:用空间向量求平面间的夹角,直线与平面垂直的判定
专题:空间角
分析:(1)以D为原点建立空间直角坐标系D-xyz,利用向量法能证明AE⊥平面SBD.
(2)分别求出平面SBD的一个法向量和平面SAB的一个法向量,利用向量法能求出二面角的余弦值.
(2)分别求出平面SBD的一个法向量和平面SAB的一个法向量,利用向量法能求出二面角的余弦值.
解答:
(1)证明:由题意知DS,DA,DC两两垂直,
∴以D为原点建立空间直角坐标系D-xyz,如图所示.
 则:D(0,0,0),A(0,a,0),B(0,a,2a),C(0,0,2a),E(0,0,
则:D(0,0,0),A(0,a,0),B(0,a,2a),C(0,0,2a),E(0,0,
),S(
a,0,0).
=(
a,0,0),
=(0,a,2a),
=(0,-a,
),
∵
∴AE⊥DS,AE⊥DB,又DS∩DB=D,
∴AE⊥平面SBD.…(7分)
(2)由(1)知
=
=(0,-a,
)为平面SBD的一个法向量.
又∵
=(0,0,2a),
=(-
a,a,0),
设平面SAB的一个法向量为m=(x,y,z),
则
,即
,
取x=1,得
=(1,
,0),…(12分)
∴cos<
,
>=
=-
.
观察知二面角A-SD-B为锐角,
∴所求的二面角的余弦值为
.…(15分)
∴以D为原点建立空间直角坐标系D-xyz,如图所示.
 则:D(0,0,0),A(0,a,0),B(0,a,2a),C(0,0,2a),E(0,0,
则:D(0,0,0),A(0,a,0),B(0,a,2a),C(0,0,2a),E(0,0,| a |
| 2 |
| 3 |
| DS |
| 3 |
| DB |
| AE |
| a |
| 2 |
∵
|
∴AE⊥DS,AE⊥DB,又DS∩DB=D,
∴AE⊥平面SBD.…(7分)
(2)由(1)知
| n |
| AE |
| a |
| 2 |
又∵
| AB |
| SA |
| 3 |
设平面SAB的一个法向量为m=(x,y,z),
则
|
|
取x=1,得
| m |
| 3 |
∴cos<
| m |
| n |
-
| ||||||
|
| ||
| 5 |
观察知二面角A-SD-B为锐角,
∴所求的二面角的余弦值为
| ||
| 5 |
点评:本题考查直线与平面垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=
如图,ABCD是边长为2的正方形,ED⊥平面ABCD,ED=1,EF∥BD且EF=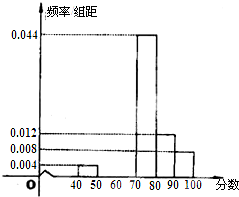 南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员.
南昌二中某学生社团为了选拔若干名社团义务宣传员,从300名志愿者中随机抽取了50名进行有关知识的测试,成绩(均为整数)按分数段分成六组:第一组[40,50),第二组[50,60),…,第六组[90,100],第一、二、三组的人数依次构成等差数列,如图是按上述分组方法得到的频率分布直方图的一部分.规定成绩不低于66分的志愿者入选为义务宣传员. 如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=
如图锐角三角形ABC的角平分线AD的延长线交它的外接圆于点E,若△ABC面积S=