题目内容
20.若sin(3π-α)=$\sqrt{2}$sin(2π+β),$\sqrt{3}$cos(-α)=-$\sqrt{2}$cos(π+β),且0<α<β<π,则sinα•sinβ=$\frac{\sqrt{2}}{4}$.分析 由条件应用诱导公式化简条件,再利用同角三角函数的基本关系求得要求式子的值.
解答 解:∵sin(3π-α)=$\sqrt{2}$sin(2π+β),∴sinα=$\sqrt{2}$•sinβ;
∵$\sqrt{3}$cos(-α)=-$\sqrt{2}$cos(π+β),∴$\sqrt{3}$cosα=$\sqrt{2}$cosβ,∴cosα=$\sqrt{\frac{2}{3}}$cosβ,
又 0<α<β<π,∴α、β都是锐角.
再根据sin2α+cos2α=2sin2β+$\frac{2}{3}$cos2β=$\frac{2}{3}$+$\frac{4}{2}$sin2β=1,求得sinβ=$\frac{1}{2}$,
∴sinα=$\sqrt{2}$•sinβ=$\frac{\sqrt{2}}{2}$,∴sinα•sinβ=$\frac{\sqrt{2}}{2}$•$\frac{1}{2}$=$\frac{\sqrt{2}}{4}$,
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题主要考查应用诱导公式化简三角函数式,同角三角函数的基本关系,属于基础题.

练习册系列答案
相关题目
15.下列图形中不一定是平面图形的是( )
| A. | 三角形 | B. | 菱形 | ||
| C. | 梯形 | D. | 四边相等的四边形 |
3.过点P(-2,0)的直线与抛物线C:y2=4x相交于A,B两点,且|PA|=$\frac{1}{2}$|AB|,则点A到抛物线C的焦点的距离为( )
| A. | $\frac{5}{3}$ | B. | $\frac{7}{5}$ | C. | $\frac{9}{7}$ | D. | 2 |
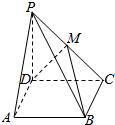 已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.
已知四棱锥P-ABCD的底面是平行四边形,如图,M是PC的中点,问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底,并说明理由.