题目内容
12.函数y=log2|ax-1|(a≠0)的图象的对称轴为直线x=-2,则a=-$\frac{1}{2}$.分析 方法一:利用含绝对值符号函数的对称性;方法二:利用特殊值法代入求出a的值即可.
解答 解:解法一:
y=log2|ax-1|=log2|a(x-$\frac{1}{a}$)|,
对称轴为x=$\frac{1}{a}$,由$\frac{1}{a}$=-2得a=-$\frac{1}{2}$.
解法二:
∵f(0)=f(-4),
可得0=log2|-4a-1|.
∴|4a+1|=1.
∴4a+1=1或4a+1=-1.
∵a≠0,
∴a=-$\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 本题考察了对数函数的对称性问题,是一道基础题.

练习册系列答案
相关题目
17.要得到y=2sin(2x+$\frac{2π}{3}$)的图象,需要将函数y=2sin(2x-$\frac{2π}{3}$)的图象( )
| A. | 向左平移$\frac{2π}{3}$个单位 | B. | 向右平移$\frac{2π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
15.已知函数$f(x)=\left\{\begin{array}{l}(2x-{x^2}){e^x},x≤0\\-{x^2}+6x+1,x>0\end{array}\right.$,g(x)=f(x)+m,若函数g(x)恰有三个不同零点,则实数m的取值范围为( )
| A. | (1,10) | B. | (-10,-1) | C. | $(0,\frac{{2\sqrt{2}+2}}{{{e^{\sqrt{2}}}}})$ | D. | $(-10,\frac{{2\sqrt{2}+2}}{{{e^{\sqrt{2}}}}})$ |
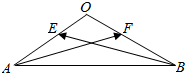 等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E,F分别是直线0A、OB上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AF}$•$\overrightarrow{AB}$=9,则μ=$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.