题目内容
5.已知x1是函数f(x)=log${\;}_{\frac{1}{2}}$x-($\frac{1}{2}$)x的零点,x2是函数g(x)=log2x-($\frac{1}{2}$)x的零点,则x1x2的取值范围是(0,1).分析 根据函数零点的性质,确定两个零点的取值范围,结合指数函数和对数函数的单调性,即可得到结论.
解答 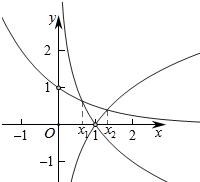 解:∵x1是函数f(x)=log${\;}_{\frac{1}{2}}$x-($\frac{1}{2}$)x的零点,x2是函数g(x)=log2x-($\frac{1}{2}$)x的零点,
解:∵x1是函数f(x)=log${\;}_{\frac{1}{2}}$x-($\frac{1}{2}$)x的零点,x2是函数g(x)=log2x-($\frac{1}{2}$)x的零点,
∴log${\;}_{\frac{1}{2}}$x1=$(\frac{1}{2})^{{x}_{1}}$,和log2x2=($\frac{1}{2}$)${\;}^{{x}_{2}}$,
则由图象可知,0<x1<1,x2>1,∴x1<x2,
则两式相减得$(\frac{1}{2})^{{x}_{1}}$-($\frac{1}{2}$)${\;}^{{x}_{2}}$=log2x1-$log_{\frac{1}{2}}}$x2=log2x1+log2x2=log2x1x2<0
即0<x1x2<1,
故答案为:(0,1).
点评 本题主要考查函数零点的应用,利用数形结合,以及指数函数和对数函数的单调性的性质是解决本题的关键.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
10.若f(x)是奇函数,且x>0时,f(x)=-x${\;}^{\frac{1}{2}}$,则当x<0时,f(x)的解析式是( )
| A. | f(x)=x${\;}^{\frac{1}{2}}$ | B. | f(x)=(-x)${\;}^{\frac{1}{2}}$ | C. | f(x)=-(-x)${\;}^{\frac{1}{2}}$ | D. | f(x)=-x${\;}^{\frac{1}{2}}$ |
17.要得到y=2sin(2x+$\frac{2π}{3}$)的图象,需要将函数y=2sin(2x-$\frac{2π}{3}$)的图象( )
| A. | 向左平移$\frac{2π}{3}$个单位 | B. | 向右平移$\frac{2π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |
8.若函数y=f(x)+cosx在[-$\frac{π}{4},\frac{3π}{4}$]上单调递减,则f(x)可以是( )
| A. | 1 | B. | -sinx | C. | cosx | D. | sinx |
9.在一次试验中,测得(x,y)的四组值分别是A(1,1.5),B(2,3),C(3,4),D(4,5.5),则y
与x之间的回归直线方程为( )
与x之间的回归直线方程为( )
| A. | $\hat y=x+1$ | B. | $\hat y=x+2$ | C. | $\hat y=2x+1$ | D. | $\hat y=x-1$ |