题目内容
11．
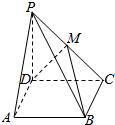已知四棱锥P-ABCD的底面是平行四边形，如图，M是PC的中点，问向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$是否可以组成一个基底，并说明理由．
分析 连结AC，BD，设AC，BD交于点O，连结MO，则MO是△PAC的中位线，于是$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$共面，不符合空间向量的基底要求．
解答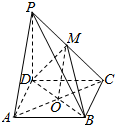 
解：连结AC，BD，设AC，BD交于点O，连结MO，则O是AC的中点，
∴MO是△PAC的中位线，∴$\overrightarrow{PA}$=2$\overrightarrow{MO}$，
∵$\overrightarrow{MB}$，$\overrightarrow{MD}$，$\overrightarrow{MO}$共面，∴$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$共面，∴向量$\overrightarrow{PA}$、$\overrightarrow{MB}$、$\overrightarrow{MD}$不能组成一个基底．
点评 本题考查了空间向量的基本定理，向量共面的判断，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
1．两圆C1：x2+y2-4x+3=0和C2：${x^2}+{y^2}+4\sqrt{3}y+3=0$的位置关系是（ ）
| A． | 相离 | B． | 相交 | C． | 内切 | D． | 外切 |
6．△ABC是边长为1的正三角形，PA⊥平面ABC，且PA=$\frac{\sqrt{6}}{4}$，点A关于平面PBC的对称点为A′，则异面直线A′C与AB所成角等于（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |
15．已知函数$f（x）=\left\{\begin{array}{l}（2x-{x^2}）{e^x}，x≤0\\-{x^2}+6x+1，x＞0\end{array}\right.$，g（x）=f（x）+m，若函数g（x）恰有三个不同零点，则实数m的取值范围为（ ）
| A． | （1，10） | B． | （-10，-1） | C． | $（0，\frac{{2\sqrt{2}+2}}{{{e^{\sqrt{2}}}}}）$ | D． | $（-10，\frac{{2\sqrt{2}+2}}{{{e^{\sqrt{2}}}}}）$ |