题目内容
15.已知f(x)=x2-2|x|(x∈R).(Ⅰ)若方程f(x)=kx有三个解,试求实数k的取值范围;
(Ⅱ)求m,n(m<n),使函数f(x)的定义域与值域均为[m,n].
分析 (Ⅰ)若方程f(x)=kx有三个解,利用函数与方程之间的关系转化为两个函数的交点个数问题,利用数形结合即可试求实数k的取值范围;
(Ⅱ)作出函数f(x)的图象,利用数形结合以及函数定义域和值域之间的关系进行求解即可.
解答 解:(Ⅰ)若方程f(x)=kx有三个解,
当x=0时,方程x2-2|x|=kx,成立,
即当x=0是方程的一个根,
当x≠0时,等价为方程x2-2|x|=kx有两个不同的根,
即k=x-$\frac{2|x|}{x}$,
设g(x)=x-$\frac{2|x|}{x}$,
则g(x)=$\left\{\begin{array}{l}{x-2,}&{x>0}\\{x+2,}&{x<0}\end{array}\right.$,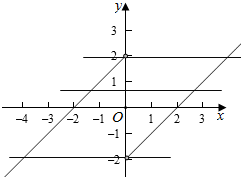
作出函数g(x)的图象如图:
则当-2<k<2时,k=x-$\frac{2|x|}{x}$有两个不同的交点,
即此时k=x-$\frac{2|x|}{x}$有两个非零的根,f(x)=kx有三个解,
综上-2<k<2.
(Ⅱ)作出函数f(x)的图象如图:
则函数f(x)的值域为[-1,+∞),
若使函数f(x)的定义域与值域均为[m,n].
则m≥-1,
若m=-1,则f(-1)=-1,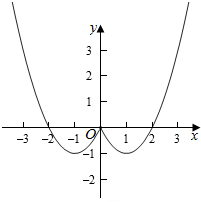
由f(x)=-1,得x=-1或x=1,
即当m=-1,n=0时,即定义域为[-1,0],此时函数的值域为[-1,0],满足条件.
由n2-2|n|=n,得,
若-1<n≤0得,n2+2n=n,
即n2+n=0,得n=0,
若0<n≤2,则函数的值域为[-1,0],
则由n2-2|n|=0,得n2-2n=0,得n=2,
若n>2,
则n2-2|n|=n,得n2-2n=n,即n2-3n=0,
得n=3,
则当m=-1,n=0时,或当m=-1,n=2,或当m=-1,n=3都满足条件.
点评 本题主要考查根的个数的判断,利用函数与方程之间的关系进行转化,利用数形结合是解决本题的关键.

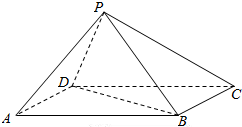 如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.
如图,四棱锥P-ABCD中,底面ABCD为矩形,AD=PD=2$\sqrt{3}$,PB=AB=6,点P在底面的正投影在DC上.(I)证明:BD⊥PA;
(Ⅱ)求直线AP与平面PBC所成角的正弦值.