题目内容
9．（2x+$\frac{1}{x}$）n的展开式的第三项系数与第四项系数相等，则二项式系数之和为（ ）| A． | 128 | B． | 36 | C． | 256 | D． | 512 |
分析 根据题意，得出2n-2•${C}_{n}^{2}$=2n-3•${C}_{n}^{3}$，化简即可求出n的值．
解答 解：∵（2x+$\frac{1}{x}$）n的展开式的第三项系数与第四项系数相等，
∴2n-2•${C}_{n}^{2}$=2n-3•${C}_{n}^{3}$，
即2•$\frac{n（n-1）}{2}$=$\frac{n（n-1）（n-2）}{6}$，
化简得n-2=6，
解得n=8；
∴二项式系数之和为28=256．
故选：C．
点评 本题考查了二项式展开式各项系数的应用问题，是基础题目．
练习册系列答案
相关题目
17．下列命题中，真命题的个数是（ ）
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直．
①经过直线外一点有且只有一条直线与已知直线平行
②经过直线外一点有且只有一条直线与已知直线垂直
③经过平面外一点有且只有一个平面与已知平面平行
④经过平面外一点有且只有一个平面与已知平面垂直．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
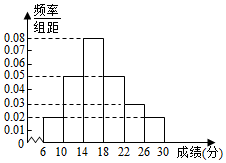某省去年高三200000名考生英语听力考试服从正态分布N（17，9），现从某校高三年级随机抽取50名考生的成绩，发现全部介于[6，30]之间，将成绩按如图方式分成6组：第1组[6，10），第2组[10，14），…，第6组[26，30），如图是按上述分组方法得到的频率分布直方图．
14．若正实数m、n满足3m+4n=5mn，则m+3n的最小值是（ ）
| A． | 4 | B． | 5 | C． | $\frac{24}{5}$ | D． | $\frac{28}{5}$ |
1．
执行如图的程序框图，若输入k=63，则输出的n=（ ）
执行如图的程序框图，若输入k=63，则输出的n=（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
18．复数z满足（z-1）（1+i）=2i，则|z|=（ ）
| A． | 1 | B． | 2 | C． | $\sqrt{5}$ | D． | 5 |
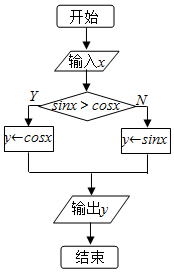如图所示的流程图，若输出的x的值为$\frac{π}{3}$，则相应输出的y值为$\frac{1}{2}$．