题目内容
19.向量$\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-3,x,y),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则x-y=-12.分析 根据空间向量的坐标表示与共线定理,列出方程求出x、y的值,计算x-y的值.
解答 解:∵向量$\overrightarrow{a}$=(1,2,-2),$\overrightarrow{b}$=(-3,x,y),且$\overrightarrow{a}$∥$\overrightarrow{b}$,
∴$\frac{-3}{1}$=$\frac{x}{2}$=$\frac{y}{-2}$,
解得x=-6,y=6,
x-y=-6-6=-12.
故答案为:-12.
点评 本题考查了空间向量的坐标表示与共线定理的应用问题,是基础题目.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
9.平面几何中,若△ABC的内切圆半径为r,其三边长分别为a,b,c,则△ABC的面积$S=\frac{1}{2}(a+b+c)•r$.类比上述命题,若三棱锥的内切球半径为R,其四个面的面积分别为S1,S2,S3,S4,猜想三棱锥体积V的一个公式.若三棱锥P-ABC的体积V=$\frac{{2\sqrt{2}}}{3}$,其四个面的面积均为$\sqrt{3}$,根据所猜想的公式计算该三棱锥P-ABC的内切球半径R为( )
| A. | $\frac{{\sqrt{6}}}{6}$ | B. | $\frac{{\sqrt{6}}}{3}$ | C. | $\frac{{\sqrt{6}}}{12}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
7.设区域Ω={(x,y)|0≤x≤2,0≤y≤2},区域A={(x,y)|xy≤1,(x,y)∈Ω},在区域Ω中随机取一个点,则该点在A中的概率( )
| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{1+2ln2}{8}$ | C. | $\frac{2ln2}{4}$ | D. | $\frac{1}{2}$ |
9.已知函数f(x)的导函数为f′(x),若?x∈(0,+∞),都有xf′(x)<2f(x)成立,则( )
| A. | 2f($\sqrt{3}$)>3f($\sqrt{2}$) | B. | 2f(1)<3f($\sqrt{2}$) | C. | 4f($\sqrt{3}$)<3f(2) | D. | 4f(1)>f(2) |
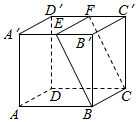 如图,在正方体中,E,F是棱A′B′与D′C′的中点,求面EBCF与面ABCD所成二面角的正切值.(取锐角)
如图,在正方体中,E,F是棱A′B′与D′C′的中点,求面EBCF与面ABCD所成二面角的正切值.(取锐角)