题目内容
12. 如图,网格纸上小方格的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小方格的边长为1,粗实线画出的是某四棱锥的三视图,则该四棱锥的表面积为( )| A. | 14+6$\sqrt{5}$ | B. | 28+6$\sqrt{5}$ | C. | 28+12$\sqrt{5}$ | D. | 36+12$\sqrt{5}$ |
分析 几何体为从正方体中切出来的四棱锥,作出直观图,计算各个面的面积.
解答 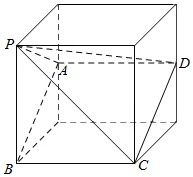 解:由三视图可知几何体是从边长为4的正方体中切出的四棱锥P-ABCD,作出直观图:
解:由三视图可知几何体是从边长为4的正方体中切出的四棱锥P-ABCD,作出直观图:
其中A,D为正方体棱的中点,P,B,C是正方体的顶点.
∴S△PAB=$\frac{1}{2}×4×4$=8,S△PBC=$\frac{1}{2}×4×4$=8,
由勾股定理可得AB=PA=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,
∴S△PAD=$\frac{1}{2}×4×2\sqrt{5}$=4$\sqrt{5}$.S矩形ABCD=4×$2\sqrt{5}$=8$\sqrt{5}$.
由勾股定理得PC=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,CD=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$,PD=$\sqrt{(4\sqrt{2})^{2}+{2}^{2}}$=6,
由余弦定理得cos∠PCD=$\frac{P{C}^{2}+C{D}^{2}-P{D}^{2}}{2PC•CD}$=$\frac{\sqrt{10}}{10}$,∴sin∠PCD=$\frac{3\sqrt{10}}{10}$.
∴S△PCD=$\frac{1}{2}×4\sqrt{2}×2\sqrt{5}×\frac{3\sqrt{10}}{10}$=12.
∴几何体的表面积为8+8+4$\sqrt{5}$+8$\sqrt{5}$+12=28+12$\sqrt{5}$.
故选C.
点评 本题考查了不规则放置的空间几何体的三视图和面积计算,以正方体为模型作出棱锥的直观图是解题关键.

练习册系列答案
相关题目
2.已知x>0,y>0,若不等式a(x+y)≥x+$\sqrt{\frac{1}{2}xy}$恒成立,则a的最小值为( )
| A. | $\frac{\sqrt{6}+2}{4}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\sqrt{6}$+2 | D. | $\sqrt{6}$+$\sqrt{2}$ |
3.幂函数的图象过点$(2,\sqrt{2})$,则该幂函数的解析式为( )
| A. | y=x-1 | B. | $y={x^{\frac{1}{2}}}$ | C. | y=x2 | D. | y=x3 |
7.设区域Ω={(x,y)|0≤x≤2,0≤y≤2},区域A={(x,y)|xy≤1,(x,y)∈Ω},在区域Ω中随机取一个点,则该点在A中的概率( )
| A. | $\frac{1+2ln2}{4}$ | B. | $\frac{1+2ln2}{8}$ | C. | $\frac{2ln2}{4}$ | D. | $\frac{1}{2}$ |
