题目内容
已知等差数列{an}中,a5=8,a10=18,三点(a1,0)、(a2,2)、(a3,0)在圆C上,
(Ⅰ)求圆C的方程;
(Ⅱ)若直线l:mx+ny+1=0被圆C所截得的弦长为2
,求m2+n2的最小值;
(Ⅲ)若一条动直线与圆C交于A、B两点,且总有|OA|•|OB|=8,(点O为坐标原点),试探究直线AB是否恒与一个定圆相切,并说明理由.
(Ⅰ)求圆C的方程;
(Ⅱ)若直线l:mx+ny+1=0被圆C所截得的弦长为2
| 3 |
(Ⅲ)若一条动直线与圆C交于A、B两点,且总有|OA|•|OB|=8,(点O为坐标原点),试探究直线AB是否恒与一个定圆相切,并说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由等差数列的性质求出a1=0,a2=2,a3=4,将三点(0,0),(2,2),(4,0)分别代入圆的一般方程,求出圆的方程为x2+y2-4x=0.
(Ⅱ)由已知得n2=3m2+4m+1,由此利用函数的单调性求出当m=-
时,(m2+n2)min=
.
(Ⅲ)设∠AOB=θ,取AB中点D,连结CD,知∠ACD=∠AOB=θ,CD⊥AB,在Rt△ACD中,|AD|=rsinθ=2sinθ,|AB|=2|AD|=4sinθ,由此能求出以点O为圆心,2为半径的圆恒与直线AB相切,圆的方程为x2+y2=4.
(Ⅱ)由已知得n2=3m2+4m+1,由此利用函数的单调性求出当m=-
| 1 |
| 3 |
| 1 |
| 9 |
(Ⅲ)设∠AOB=θ,取AB中点D,连结CD,知∠ACD=∠AOB=θ,CD⊥AB,在Rt△ACD中,|AD|=rsinθ=2sinθ,|AB|=2|AD|=4sinθ,由此能求出以点O为圆心,2为半径的圆恒与直线AB相切,圆的方程为x2+y2=4.
解答:
解:(Ⅰ)设等差数列的公差为d,则5d=a10-a5=10,解得d=2,
∴an=a5+(n-5)d=8+2(n-5)=2n-2,
解得a1=0,a2=2,a3=4,
将三点(0,0),(2,2),(4,0)分别代入圆的一般方程:
x2+y2+Dx+Ey+F=0,得:
,解得
,
∴圆的方程为x2+y2-4x=0.
(Ⅱ)由已知得
=
,化简,得n2=3m2+4m+1,
∵n2≥0,∴(3m+1)(m+1)≥0,解得m≥-
,或m≤-1.
∵m2+n2=4m2+4m+1=(2m+1)2,m≥-
或m≤-1,
又4m2+4m+1在m≥-
单调增,在m≤-1单调减,
∴当m=-
时,(m2+n2)min=
.
(Ⅲ)设∠AOB=θ,取AB中点D,
连结CD,则可知∠ACD=∠AOB=θ,CD⊥AB,
在Rt△ACD中,|AD|=rsinθ=2sinθ,
∴|AB|=2|AD|=4sinθ,
∵S△AOB=
|OA|•|OB|sinθ
=
|AB|d,(d为点O到直线AB的距离).
又|OA|•|OB|=8,解得d=2,
∵定点O到动直线AB的距离d=2,
∴以点O为圆心,2为半径的圆恒与直线AB相切,圆的方程为x2+y2=4.
∴an=a5+(n-5)d=8+2(n-5)=2n-2,
解得a1=0,a2=2,a3=4,
将三点(0,0),(2,2),(4,0)分别代入圆的一般方程:
x2+y2+Dx+Ey+F=0,得:
|
|
∴圆的方程为x2+y2-4x=0.
(Ⅱ)由已知得
| |2m+1| | ||
|
| 4-3 |
∵n2≥0,∴(3m+1)(m+1)≥0,解得m≥-
| 1 |
| 3 |
∵m2+n2=4m2+4m+1=(2m+1)2,m≥-
| 1 |
| 3 |
又4m2+4m+1在m≥-
| 1 |
| 3 |

∴当m=-
| 1 |
| 3 |
| 1 |
| 9 |
(Ⅲ)设∠AOB=θ,取AB中点D,
连结CD,则可知∠ACD=∠AOB=θ,CD⊥AB,
在Rt△ACD中,|AD|=rsinθ=2sinθ,
∴|AB|=2|AD|=4sinθ,
∵S△AOB=
| 1 |
| 2 |
=
| 1 |
| 2 |
又|OA|•|OB|=8,解得d=2,
∵定点O到动直线AB的距离d=2,
∴以点O为圆心,2为半径的圆恒与直线AB相切,圆的方程为x2+y2=4.
点评:本题考查圆的方程的求法,考查最小值的求法,探究圆的方程量否存在及求法,解题时要注意数列、不等式、三角函数、圆等知识点的合理运用.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
若α是第二象限角,且tan(π-α)=
,则cos(
-α)=( )
| 1 |
| 2 |
| 3π |
| 2 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
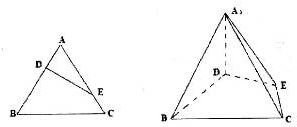 已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足
已知等边三角形的边长为3,点D,E分别在边AB,AC上,且满足