题目内容
设函数fn(x)=x-
+
-…+(-1)n-1
,(x∈[0,1],n∈N*),则( )
| x3 |
| 3! |
| x5 |
| 5! |
| x2n-1 |
| (2n-1)! |
| A、f2(x)≤sinx≤f3(x) |
| B、f3(x)≤sinx≤f2(x) |
| C、sinx≤f2(x)≤f3(x) |
| D、f2(x)≤f3(x)≤sinx |
考点:二项式定理的应用
专题:二项式定理
分析:构造函数F(x)=sinx-f2(x),利用导数可得F(x)是[0 1]内的增函数,F(x)≥0,即f2(x)≤sinx.同理f3(x)≥sinx,从而得到sinx、f2(x)、f3(x)的大小关系.
解答:
解:∵函数fn(x)=x-
+
-…+(-1)n-1
,(x∈[0,1],n∈N*),
则f2(x)=x-
,f3(x)=x-
+
,显然f2(x)≤f3(x).
构造函数F(x)=sinx-f2(x)=sinx-x+
,其中0≤x≤1,且F(0)=0.
所以F'(x)=cosx-1+
,且F'(0)=0,
F''(x)=-sinx+x=x-sinx≥0恒成立,
所以F'(x)递增,所以F'(x)≥F'(0)=0,所以F(x)是[0 1]内的增函数,F(x)≥0,
即sinx-f2(x)≥0恒成立,所以,f2(x)≤sinx.
同理可证:f3(x)≥sinx,
故选:A.
| x3 |
| 3! |
| x5 |
| 5! |
| x2n-1 |
| (2n-1)! |
则f2(x)=x-
| x3 |
| 6 |
| x3 |
| 6 |
| x5 |
| 120 |
构造函数F(x)=sinx-f2(x)=sinx-x+
| x3 |
| 6 |
所以F'(x)=cosx-1+
| x2 |
| 2 |
F''(x)=-sinx+x=x-sinx≥0恒成立,
所以F'(x)递增,所以F'(x)≥F'(0)=0,所以F(x)是[0 1]内的增函数,F(x)≥0,
即sinx-f2(x)≥0恒成立,所以,f2(x)≤sinx.
同理可证:f3(x)≥sinx,
故选:A.
点评:本题主要考查比较几个数的大小的方法,利用导数研究函数的单调性,由单调性求函数的最值,体现了转化的数学思想,属于基础题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
下列结论正确的是( )
A、若向量
| ||||||||||||
B、已知向量
| ||||||||||||
C、“若 θ=
| ||||||||||||
| D、若命题 p:?x∈R,x2-x+1<0,则?p:?x∈R,x2-x+1>0 |
 已知椭圆
已知椭圆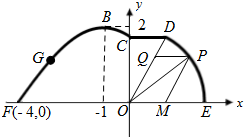 如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧
如图,在海岸线EF一侧有一休闲游乐场,游乐场的前一部分边界为曲线段FGBC,该曲线段是函数y=Asin(ωx+ϕ)(A>0,ω>0,ϕ∈(0,π)),x∈[-4,0]的图象,图象的最高点为B(-1,2).边界的中间部分为长1千米的直线段CD,且CD∥EF.游乐场的后一部分边界是以O为圆心的一段圆弧