题目内容
120°= rad，与它终边相同的角的集合为 ．
考点：终边相同的角,弧度与角度的互化
专题：三角函数的求值
分析：直接利用角度与弧度的换算关系以及终边相同的角的表示方法求解即可．
解答：
解：因为π=180°，所以120°=
．
与120°终边相同的角的集合为：{α|α=k•360°+120°，k∈Z}．
故答案为：
；{α|α=k•360°+120°，k∈Z}．
| 2π |
| 3 |
与120°终边相同的角的集合为：{α|α=k•360°+120°，k∈Z}．
故答案为：
| 2π |
| 3 |
点评：本题考查角度与弧度的互化，终边相同角的表示方法，基本知识的考查．
练习册系列答案
阅读快车系列答案
相关题目
设函数fn（x）=x-
+
-…+（-1）n-1
，（x∈[0，1]，n∈N*），则（ ）
| x3 |
| 3! |
| x5 |
| 5! |
| x2n-1 |
| (2n-1)! |
| A、f2（x）≤sinx≤f3（x） |
| B、f3（x）≤sinx≤f2（x） |
| C、sinx≤f2（x）≤f3（x） |
| D、f2（x）≤f3（x）≤sinx |
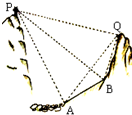如图，为了测量两座山峰上两点P、Q之间的距离，选择山坡上一段长度为300