题目内容
求下列函数的定义域：y=
．
| 1 | ||
|
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据使函数y=
的解析式有意义的原则，构造关于自变量x的不等式x2-3＞0，解得函数的定义域．
| 1 | ||
|
解答：
解：要使函数y=
的解析式有意义，
自变量x须满足x2-3＞0，
解得：x∈（-∞，-
）∪（
，+∞），
故函数的定义域为：（-∞，-
）∪（
，+∞），
| 1 | ||
|
自变量x须满足x2-3＞0，
解得：x∈（-∞，-
| 3 |
| 3 |
故函数的定义域为：（-∞，-
| 3 |
| 3 |
点评：本题考查的知识点是函数的定义域及其求法，其中根据使函数y=
的解析式有意义的原则，构造关于自变量x的不等式x2-3＞0，是解答的关键．
| 1 | ||
|
练习册系列答案
通城学典默写能手系列答案
相关题目
若复数z满足（3+4i）z=|4-3i|，则复数z对应的点位于（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设函数fn（x）=x-
+
-…+（-1）n-1
，（x∈[0，1]，n∈N*），则（ ）
| x3 |
| 3! |
| x5 |
| 5! |
| x2n-1 |
| (2n-1)! |
| A、f2（x）≤sinx≤f3（x） |
| B、f3（x）≤sinx≤f2（x） |
| C、sinx≤f2（x）≤f3（x） |
| D、f2（x）≤f3（x）≤sinx |
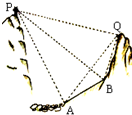如图，为了测量两座山峰上两点P、Q之间的距离，选择山坡上一段长度为300