��Ŀ����
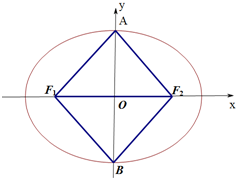 ��ͼ������ԲC��
��ͼ������ԲC��| x2 |
| a2 |
| y2 |
| a2 |
| F1A |
| F1B |
| F2A |
| F2B |
| 2 |
��������ԲC�ı����̣�
���������M��
| 2 |
| 3 |
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺�ۺ���,Բ���ߵĶ��塢�����뷽��
��������I����|
+
|=|
-
|��2b=2c����b=c��������ԲC�����㣨
��1�����������������������ԲC�ı����̣�
���������ۣ���l�ķ���Ϊy=k��x-
����������Բ���̣�����Τ�ﶨ����֤��
•
=0�����ɵó����ۣ�
| F1A |
| F1B |
| F2A |
| F2B |
| 2 |
���������ۣ���l�ķ���Ϊy=k��x-
| 2 |
| 3 |
| PT |
| QT |
���
�⣺��I������Բ�İ뽹��Ϊc��c��0������|
+
|=|
-
|��2b=2c����b=c��
��a2=b2+c2=2b2��
����ԲC�����㣨
��1����
��
+
=1��
��b2=2��a2=4��
����ԲC�ı�����Ϊ
+
=1��
��II����ֱ��l��x�ᴹֱʱ����x=
���뵽��ԲC�ı������е�y=��
��
��
+
=2�������T��2��0������������
ֱ��l��x���ֱʱ������б��Ϊk������֤������kΪ��ֵ��T��2��0������������
��P��x1��y1����Q��x2��y2����������l�ķ���Ϊy=k��x-
����
������Բ���̣���ȥy���ɵã�1+2k2��x2-
k2x+
k2-4=0��
��x1+x2=
��x1x2=
��
��
•
=��1+k2��x1x2-��2+k2����x1+x2��+
k2+4=0��
������kΪ��ֵ��
•
=0������PQΪֱ����Բ�������T��2��0����
| F1A |
| F1B |
| F2A |
| F2B |
��a2=b2+c2=2b2��
����ԲC�����㣨
| 2 |
��
| 2 |
| 2b2 |
| 1 |
| b2 |
��b2=2��a2=4��
����ԲC�ı�����Ϊ
| x2 |
| 4 |
| y2 |
| 2 |
��II����ֱ��l��x�ᴹֱʱ����x=
| 2 |
| 3 |
| 4 |
| 3 |
��
| 4 |
| 3 |
| 2 |
| 3 |
ֱ��l��x���ֱʱ������б��Ϊk������֤������kΪ��ֵ��T��2��0������������
��P��x1��y1����Q��x2��y2����������l�ķ���Ϊy=k��x-
| 2 |
| 3 |
������Բ���̣���ȥy���ɵã�1+2k2��x2-
| 8 |
| 3 |
| 8 |
| 9 |
��x1+x2=
| ||
| 1+2k2 |
| ||
| 1+2k2 |
��
| PT |
| QT |
| 4 |
| 9 |
������kΪ��ֵ��
| PT |
| QT |
���������⿼����Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ����������֪ʶ�����ã������е��⣮

��ϰ��ϵ�д�
�����Ŀ
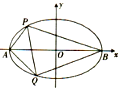 ��ͼ����
��ͼ����