题目内容
7.已知函数f(x)=$\left\{\begin{array}{l}1-|x+1|,x∈[-2,0]\\ 2f(x-2),x∈(0,+∞).\end{array}$(1)求函数f(x)在[-2,4]上的解析式;
(2)若方程f(x)=x+a在区间[-2,4]内有3个不等实根,求实数a的取值范围.
分析 (1)利用函数的递推关系式,求解分段函数的解析式即可.
(2)画出函数的图象,利用函数的零点的个数推出a 的范围即可.
解答 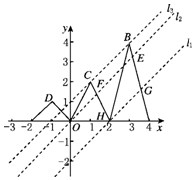 解:(1)函数f(x)=$\left\{\begin{array}{l}1-|x+1|,x∈[-2,0]\\ 2f(x-2),x∈(0,+∞).\end{array}$,
解:(1)函数f(x)=$\left\{\begin{array}{l}1-|x+1|,x∈[-2,0]\\ 2f(x-2),x∈(0,+∞).\end{array}$,
x∈(0,2]时,x-2∈(-2,0),可得f(x)=2(1-|x-1|)=2-2|x-1|.
x∈(2,4]时,x-2∈(0,2),可得f(x)=2(2-2|x-3|)=4-4|x-3|,
,∴当-2≤x≤4时,f(x)=$\left\{\begin{array}{l}{1-|x+1|,x∈[-2,0]}\\{2-2|x-1|,x∈(0,2]}\\{4-4|x-3|,x∈(2,4]}\end{array}\right.$.
(2)作出函数f(x)在区间[-2,4]上的图象,如图所示.
设y=x+a,由图象可知要使方程f(x)=x+a在区间[-2,4]内有3个不等实根,
则直线y=x+a应位于l1与l2之间或直线l3的位置,
所以实数a的取值范围是-2<a<0或a=1.
点评 本题考查函数的图象的应用,函数的零点与方程根的关系,函数的解析式的求法,考查数形结合以及只好思想的应用.

练习册系列答案
相关题目
15.已知双曲线的中心在原点,两个焦点F1,F2分别为$(-\sqrt{5},0)和(\sqrt{5},0)$,点P在双曲线上,PF1⊥PF2,且△PF1F2的面积为1,则双曲线的方程为( )
| A. | $\frac{x^2}{2}-\frac{y^2}{3}=1$ | B. | $\frac{x^2}{3}-\frac{y^2}{2}=1$ | C. | $\frac{x^2}{4}-{y^2}=1$ | D. | ${x^2}-\frac{y^2}{4}=1$ |
2.已知i是复数的虚数单位,若复数z(1+i)=|2i|,则复数z=( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | i |
12.已知正实数a,b满足a+b=3,则$\frac{1}{a}+\frac{4}{5+b}$的最小值为( )
| A. | 1 | B. | $\frac{7}{8}$ | C. | $\frac{9}{8}$ | D. | 2 |
16.已知Sn是公比为q的等比数列{an}的前n项和.若3S1,2S2,S3成等差数列,则q=( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 3 |
 如图所示,在△ABC中,I为△ABC的内心,AI交BC于D,交△ABC外接圆于E
如图所示,在△ABC中,I为△ABC的内心,AI交BC于D,交△ABC外接圆于E