题目内容
设f(x)是定义在R上的偶函数,对x∈R,都有f(x-2)=f(x+2),且当x∈[-2,0]时,f(x)=(
)x-1,若在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实根,则a的取值范围是( )
| 1 |
| 2 |
| A、(1,2) | |||
| B、(2,+∞) | |||
C、(1,
| |||
D、(
|
考点:函数的零点与方程根的关系
专题:作图题,函数的性质及应用
分析:作出在区间(-2,6]内函数f(x)的图象,将方程的根的个数化为函数图象交点的个数.
解答:
解:∵f(x)是定义在R上的偶函数,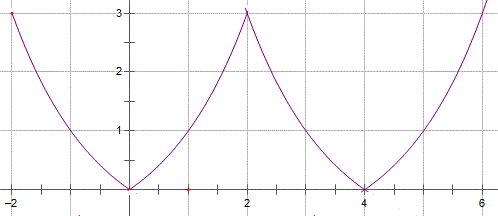
∴f(x)的图象关于y轴对称,
∵对x∈R,都有f(x-2)=f(x+2),
∴f(x)是周期函数,且周期为4;
∵当x∈[-2,0]时,f(x)=(
)x-1,
∴其在区间(-2,6]内的图象如右图,
∴在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实根可转化为,函数f(x)的图象与y=loga(x+2)的图象有且只有三个不同的交点,
则loga(2+2)<3,且loga(6+2)>3
解得,a∈(
,2).
故选D.

∴f(x)的图象关于y轴对称,
∵对x∈R,都有f(x-2)=f(x+2),
∴f(x)是周期函数,且周期为4;
∵当x∈[-2,0]时,f(x)=(
| 1 |
| 2 |
∴其在区间(-2,6]内的图象如右图,
∴在区间(-2,6]内关于x的方程f(x)-loga(x+2)=0(a>1)恰有3个不同的实根可转化为,函数f(x)的图象与y=loga(x+2)的图象有且只有三个不同的交点,
则loga(2+2)<3,且loga(6+2)>3
解得,a∈(
| 3 | 4 |
故选D.
点评:本题通过分析可得函数f(x)的性质,并由这些性质根据图象变换作出其图象,将方程问题化为图象交点问题,属于中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
下列给出的赋值语句中正确的是( )
| A、3=A | B、x=-x |
| C、B=A=2 | D、x+y=0 |
在抛物线y2=4x上恒有两点关于直线l:y=kx+3则对称,k的取值范围是( )
| A、-1<k<0 |
| B、0<k<1 |
| C、-1≤k≤0 |
| D、0≤k≤1 |
设变量x、y满足约束条件
,则z=2x+3y的最大值为( )
|
| A、18 | B、2 | C、3 | D、0 |
直线x+
y-m=0与圆x2+y2=1在第一象限内有两个不同的交点,则m的取值范围是( )
| 3 |
| A、(1,2) | ||
B、(
| ||
C、(1,
| ||
D、(
|
复数Z=
,则复数
对应的点在( )
| ||
1-
|
. |
| Z |
| A、第一象限或第三象限 |
| B、y轴负半轴上 |
| C、x轴正半轴上 |
| D、第二象限或第四象限 |
已知0<b<1,0<α<
,x=(sinα)logbsinα,y=(cosα)logbcosα,z=(sinα)logbcosα则三数的大小关系是( )
| π |
| 4 |
| A、x<y<z |
| B、z<x<y |
| C、x<z<y |
| D、y<z<x |