题目内容
某人年初向银行贷款10万元用于购房,
(1)如果他向建设银行贷款,年利率为5%,且这笔款分10次等额归还(不计复利),每年一次,并从借后次年年初开始归还,问每年应付多少元?
(2)如果他向工商银行贷款,年利率为4%,要按复利计算(即本年的利息计入次年的本金生息),仍分10次等额归还,每年一次,每年应还多少元?(其中:1.0410=1.4802)
(1)如果他向建设银行贷款,年利率为5%,且这笔款分10次等额归还(不计复利),每年一次,并从借后次年年初开始归还,问每年应付多少元?
(2)如果他向工商银行贷款,年利率为4%,要按复利计算(即本年的利息计入次年的本金生息),仍分10次等额归还,每年一次,每年应还多少元?(其中:1.0410=1.4802)
考点:函数模型的选择与应用
专题:计算题,应用题,函数的性质及应用
分析:(1)设每年还款x元,由题意可得105(1+10×5%)=x(1+9×5%)+x(1+8×5%)+…+x,从而解x;
(2)设每所还款y元,由题意可得105(1+4%)10=y(1+4%)9+y(1+4%)8+…+y,从而解y.
(2)设每所还款y元,由题意可得105(1+4%)10=y(1+4%)9+y(1+4%)8+…+y,从而解y.
解答:
解:(1)设每年还款x元,
则105(1+10×5%)=x(1+9×5%)+x(1+8×5%)+…+x,
即105×1.5=10x+45•0.05x,
解得,x=
≈12245(元);
(2)设每所还款y元,
则105(1+4%)10=y(1+4%)9+y(1+4%)8+…+y,
即105×1.0410=y
,
则y≈
≈12330(元).
则105(1+10×5%)=x(1+9×5%)+x(1+8×5%)+…+x,
即105×1.5=10x+45•0.05x,
解得,x=
| 105×1.5 |
| 12.25 |
(2)设每所还款y元,
则105(1+4%)10=y(1+4%)9+y(1+4%)8+…+y,
即105×1.0410=y
| 1.0410-1 |
| 1.04-1 |
则y≈
| 105×1.4802×0.04 |
| 0.4802 |
点评:本题考查了实际问题转化为数学问题的能力,属于中档题.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
已知幂函数y=(m2-5m-5)x2m+1在(0,+∞)单调递减,则实数m=( )
| A、1 | B、-1 | C、6 | D、-1或6 |
| 2cos20°-1 |
| cos20°sin220° |
A、
| ||
B、2-
| ||
| C、4 | ||
| D、8 |
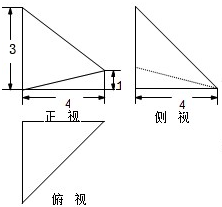 已知一个几何体的三视图如图所示,其中正视图是直角梯形.
已知一个几何体的三视图如图所示,其中正视图是直角梯形.