题目内容
3.已知$\overrightarrow{a}$=(1,0),|$\overrightarrow{b}$|=$\sqrt{2}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|,则$\overrightarrow{a}$,$\overrightarrow{b}$的夹角是( )| A. | $\frac{π}{2}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{6}$ |
分析 由条件利用两个向量的数量积的定义,求得cosθ的值,可得设$\overrightarrow{a}$与$\overrightarrow{b}$夹角θ的值.
解答 解:已知$\overrightarrow{a}$=(1,0),|$\overrightarrow{b}$|=$\sqrt{2}$,|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$|,
设$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为θ,θ∈[0,π],
则${\overrightarrow{a}}^{2}$+${\overrightarrow{b}}^{2}$-2$\overrightarrow{a}•\overrightarrow{b}$=${\overrightarrow{a}}^{2}$,∴${\overrightarrow{b}}^{2}$=2$\overrightarrow{a}$•$\overrightarrow{b}$,
∴2=2•1•$\sqrt{2}$cosθ,∴cosθ=$\frac{\sqrt{2}}{2}$,∴θ=$\frac{π}{4}$,
故选:C.
点评 本题主要考查两个向量的数量积的定义,属于基础题.

练习册系列答案
相关题目
13.若复数z满足iz=1+3i,则复数z的虚部为( )
| A. | -1 | B. | -i | C. | 1 | D. | i |
15.当x+y+z=1时,则x2+y2+z2的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{27}$ | D. | 3 |
12. 下面的茎叶图记录了甲、乙两名同学在10次英语听力比赛中的成绩(单位:分),已知甲得分的中位数为76分,乙得分的平均数是75分,则下列结论正确的是( )
下面的茎叶图记录了甲、乙两名同学在10次英语听力比赛中的成绩(单位:分),已知甲得分的中位数为76分,乙得分的平均数是75分,则下列结论正确的是( )
 下面的茎叶图记录了甲、乙两名同学在10次英语听力比赛中的成绩(单位:分),已知甲得分的中位数为76分,乙得分的平均数是75分,则下列结论正确的是( )
下面的茎叶图记录了甲、乙两名同学在10次英语听力比赛中的成绩(单位:分),已知甲得分的中位数为76分,乙得分的平均数是75分,则下列结论正确的是( )| A. | $\overline{x_甲}=76,\overline{x_乙}=75$ | B. | 乙同学成绩较为稳定 | ||
| C. | 甲数据中x=3,乙数据中y=6 | D. | 甲数据中x=6,乙数据中y=3 |
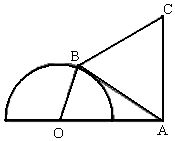 如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.当四边形OACB面积最大时,∠AOB=150°.
如图,半圆O的直径为2,A为直径延长线上的一点,OA=2,B为半圆上任意一点,以AB为一边作等边三角形ABC.当四边形OACB面积最大时,∠AOB=150°.