题目内容
已知函数f(x)对任意x、y∈R,都有f(x+y)=f(x)+f(y),且x>0时,f(x)<0,f(1)=-2.
(1)求证:f(x)是奇函数;
(2)求f(x)在[-3,3]上的最大值和最小值.
(1)证明:令x=y=0,知f(0)=0;再令y=-x,则f(0)=f(x)+f(-x)=0,∴f(-x)=-f(x),
∴f(x)为奇函数.
(2)解:对任意x1、x2∈[-3,3],设x1<x2,则x2-x1>0,∴f(x2-x1)=f[x2+(-x1)]=f(x2)+f(-x1)=f(x2)-f(x1)<0,∴f(x)为减函数.而f(3)=f(2+1)=f(2)+f(1)=3f(1)=-6,f(-3)=-f(3)=6.
∴f(x)max=f(-3)=6,f(x)min=f(3)=-6.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 的值域为________.
的值域为________. +a是奇函数,则a=______.
+a是奇函数,则a=______.
 +y2=1,若函数y=f(x)的值域是(-1,1),则f(x)一定是( )
+y2=1,若函数y=f(x)的值域是(-1,1),则f(x)一定是( )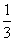 x2+10x(万元);当年产量不小于80千件时,C(x)=51x+
x2+10x(万元);当年产量不小于80千件时,C(x)=51x+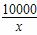 -1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.