题目内容
已知函数f（x）是定义在R上的单调增函数，且满足对任意的实数x都有f[f（x）-3x]=4，则f（x）+f（-x） 的最小值等于（ ）
| A、2 | B、4 | C、8 | D、12 |
考点：函数单调性的性质
专题：函数的性质及应用
分析：先求出函数的表达式f（x）=3x+c，得到3c+c=4，求出c的值，由f（x）+f（-x）=3x+c+3-x+c≥2
+2c，将c=1代入即可求出答案．
| 3x•3-x |
解答：
解：任意的x属于R都有有 f （ f （x）-3x ）=4，
而函数是单调的，所以对任何的x，f （x）-3x为定值c，
即f（x）=3x+c，
f（f（x）-3x）=f（c）=4
而f（c）=3c+c，
所以3c+c=4，
解得：c=1，
而f（x）+f（-x）=3x+c+3-x+c≥2
+2c=2+2=4，
故选：B．
而函数是单调的，所以对任何的x，f （x）-3x为定值c，
即f（x）=3x+c，
f（f（x）-3x）=f（c）=4
而f（c）=3c+c，
所以3c+c=4，
解得：c=1，
而f（x）+f（-x）=3x+c+3-x+c≥2
| 3x•3-x |
故选：B．
点评：本题考查了函数的单调性问题，考查了转化思想，考查了函数的最值问题，是一道中档题．
练习册系列答案
相关题目
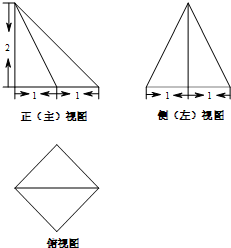某四棱锥的三视图如图所示，其中正（主）视图是等腰直角三角形，侧（左）视图是等腰三角形，俯视图是正方形，则该四棱锥的体积是（ ）圆x2+y2-4x-4y-1=0上的动点P到直线x+y=0的最小距离为（ ）
| A、1 | ||
| B、0 | ||
C、2
| ||
D、2
|
执行如图所示的程序框图，如果输入-2，那么输出的结果是