题目内容
已知直线l的方程为3x-4y+12=0,则l与两坐标轴围成的三角形的内切圆方程为 .
考点:直线与圆的位置关系
专题:直线与圆
分析:分别直线和坐标轴的交点坐标,设△AOB的内切圆的圆心(a,b),再由相切列出方程求出a、b的值,代入圆的标准方程即可.
解答:
解:直线3x-4y+12=0与坐标轴的交点坐标为(-4,0)和(0,3),
设△AOB的内切圆的圆心(a,b),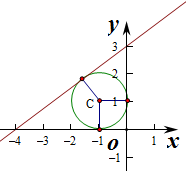 (-4<a<0,0<b<3)
(-4<a<0,0<b<3)
∵内切圆与x、y轴都相切,所以r=|a|=|b|,
∴a=-r,b=r,即圆心(-r,r),
又内切圆与直线3x+4y-12=0相切,
∴圆心到直线3x-4y+12=0距离d=
=
=r,
解得r=1,则圆心为(-1,1),
则△AOB的内切圆的方程为:(x+1)2+(y-1)2=1,
故答案为:(x+1)2+(y-1)2=1.
设△AOB的内切圆的圆心(a,b),
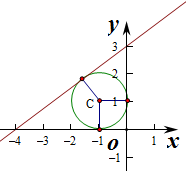 (-4<a<0,0<b<3)
(-4<a<0,0<b<3)∵内切圆与x、y轴都相切,所以r=|a|=|b|,
∴a=-r,b=r,即圆心(-r,r),
又内切圆与直线3x+4y-12=0相切,
∴圆心到直线3x-4y+12=0距离d=
| |-3r-4r+12| |
| 5 |
| |12-7r| |
| 5 |
解得r=1,则圆心为(-1,1),
则△AOB的内切圆的方程为:(x+1)2+(y-1)2=1,
故答案为:(x+1)2+(y-1)2=1.
点评:本题主要考查圆的方程求法,利用待定系数法,以及直线与圆相切的条件是解决本题的关键.,属于中档题.

练习册系列答案
相关题目
棱长为2的正方体的外接球的表面积为( )
| A、4π | B、12π |
| C、24π | D、48π |
曲线y=
+1(-2≤x≤2)与直线y=kx-2k+4有两个不同的交点时实数k的范围是( )
| 4-x2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-∞,
|
已知等比数列{an}的各项均为正数,且a2,
a3,2a1成等差数列,则该数列的公比为( )
| 1 |
| 2 |
A、1+
| ||
B、1±
| ||
| C、-1 | ||
| D、1 |
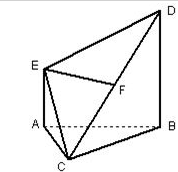 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.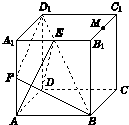 如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F、M分别是棱A1B1、AA1、B1C1的中点.