Question

近年来，我国许多地方出现雾霾天气，影响了人们的出行、工作与健康．其形成与 PM2.5有关．PM2.5是指大气中直径小于或等于2.5微米的颗粒物，也称为可入肺颗粒物．PM2.5日均值越小，空气质量越好．为加强生态文明建设，我国国家环保部于2012年2月29日，发布了《环境空气质量标准》见下表：

PM2.5日均值k（微克）	空气质量等级
k≤35	一级
35＜k≤75	二级
k＞75	超标

某环保部门为了了解甲、乙两市的空气质量状况，在某月中分别随机抽取了甲、乙两市6天的 PM2.5日均值作为样本，样本数据茎叶图如图所示（十位为茎，个位为叶）．
（Ⅰ）求甲、乙两市PM2.5日均值的样本平均数，据此判断该月中哪个市的空气质量较好；
（Ⅱ）若从甲市这6天的样本数据中随机抽取两天的数据，求恰有一天空气质量等级为一级的概率．

Answer 1

考点：古典概型及其概率计算公式,茎叶图

专题：概率与统计

分析：（Ⅰ）分别甲、乙两市PM2.5日均值的样本的和除以样本数量，求出样本的平均数即可；结合《环境空气质量标准》表，判断该月中哪个市的空气质量较好即可；
（Ⅱ）列举出甲市这6天的样本数据中随机抽取两天的所有情况，以及“恰有一天空气质量等级为一级”这个事件包含的情况，后者除以前者，求出恰有一天空气质量等级为一级的概率即可．

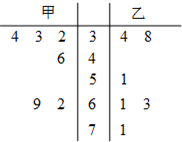
解答： 解析：（Ⅰ）甲市抽取的样本数据分别是32，33，34，46，62，69，
乙市抽取的样本数据分别是34，38，51，61，63，71，

.

x

甲=

32+33+34+46+62+69

6

=46，

.

x

乙=

34+38+51+61+63+71

6

=53；
因为

.

x

甲＜

.

x

乙，
所以甲市的空气质量较好．
（Ⅱ）由茎叶图知，甲市6天中有3天空气质量等级为一级，有3天空气质量等级为二级，
空气质量等级为一级的三天数据为a₁，a₂，a₃，空气质量等级为二级的3天数据为b₁，b₂，b₃，
则6天中抽取两天的所有情况为：a₁a₂，a₁a₃，a₁b₁，a₁b₂，a₁b₃，a₂a₃，a₂b₁，a₂b₂，a₂b₃，a₃b₁，a₃b₂，a₃b₃，b₁b₂，b₁b₃，b₂b₃．
即基本事件总数为15；                                                  
记“恰有一天空气质量等级为一级”为事件A，
则事件A包含的基本事件为：a₁b₁，a₁b₂，a₁b₃，a₂b₁，a₂b₂，a₂b₃，a₃b₁，a₃b₂，a₃b₃，
即事件A包含的事件数为9；                                                           
所以P(A)=

9

15

=

3

5

，
即恰有一天空气质量等级为一级的概率为

3

5

．

点评：本题主要考查了概率的求法，考查了样本平均数的求法，以及学生的分析推理能力和运算能力，解答此题的关键是要弄清楚两点：①符合条件的情况数目；②全部情况的总数；二者的比值就是其发生的概率的大小．