题目内容
15.求函数y=$\sqrt{3}$cos2x+sin2x+1的最大值和最小值,并指出当x取何值时,函数取得最大值和最小值.分析 利用两角和与差的三角函数化简函数为一个角的一个三角函数的形式,然后可得答案.
解答 解:函数y=$\sqrt{3}$cos2x+sin2x+1=2sin(2x+$\frac{π}{3}$)+1,
当2x+$\frac{π}{3}$=$\frac{π}{2}$+2kπ,k∈Z,即x=$\frac{π}{12}$+kπ,k∈Z时,函数取得最大值3,
当2x+$\frac{π}{3}$=-$\frac{π}{2}$+2kπ,k∈Z,即x=$-\frac{5π}{12}$+kπ,k∈Z时,函数取得最小值-1.
点评 本题考查的知识点是正弦型函数的图象和性质,和差角(辅助角)公式,难度中档.

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
6.“0<a<3”是“双曲线$\frac{{x}^{2}}{a}$-$\frac{{y}^{2}}{9}$=1(a>0)的离心率大于2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
10.点A为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点,过右焦点F(1,0)且倾斜角为$\frac{π}{6}$的直线与直线x=a2交于点P.若△APF为等腰三角形,则双曲线的离心率为( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{3}$ |
20.己知tanx=2,则$\frac{5sinx-cosx}{2sinx+cosx}$=( )
| A. | $\frac{6}{5}$ | B. | $\frac{9}{5}$ | C. | $\frac{8}{5}$ | D. | $\frac{7}{5}$ |
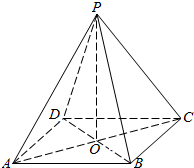 如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求:
如图,O为正四棱锥P-ABCD的底面中心,该棱锥的侧棱长和底面边长都是2.试求: