题目内容
5.已知函数$f(x)=\left\{\begin{array}{l}{(\frac{1}{2})^x}-2\;\;,\;x≤-1,\;\\(x-2)(|x|-1)\;,x>-1.\end{array}\right.$,则f(f(-2))=0,若f(x)≥2,则x的取值范围为x≥3或x=0或x≤-2.分析 由分段函数的表达式,利用代入法即可求第一问,讨论x的取值范围,解不等式即可求第二问.
解答 解:由分段函数的表达式得f(-2)=$(\frac{1}{2})^{-2}-2$=4-2=2,
f(2)=0,故f(f(-2))=0,
若x≤-1,由f(x)≥2得($\frac{1}{2}$)x-2≥2得($\frac{1}{2}$)x≥4,则2-x≥4,
得-x≥2,则x≤-2,此时x≤-2.
若x>-1,由f(x)≥2得(x-2)(|x|-1)≥2,
即x|x|-x-2|x|≥0,
若x≥0得x2-3x≥0,则x≥3或x≤0,此时x≥3或x=0,
若x<0,得-x2+x≥0,得x2-x≤0,得0≤x≤1,此时无解,
综上x≥3或x=0,或x≤-2
故答案为:0,x≥3或x=0或x≤-2
点评 本题主要考查函数值的计算,根据分段函数的表达式分别利用代入法和分类讨论的思想是解决本题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
16.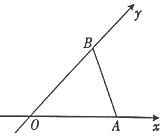 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )
 用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )
用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形,其中OA=OB=1,则原平面图形的面积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{3}{2}$ | D. | 2 |
13.直线l在平面α内,直线m平行于平面α,且与直线l异面,动点P在平面α上,且到直线l、m距离相等,则点P的轨迹为( )
| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
10.若O为坐标原点,已知实数x,y满足条件$\left\{\begin{array}{l}x+y≥1\\ x-y≥-1\\ 2x-y≤2\end{array}\right.$,在可行域内任取一点P(x,y),则|OP|的最小值为( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{3}{2}$ |
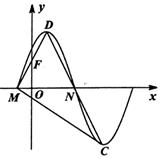 如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.
如图是函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<$\frac{π}{2}$)的部分图象,M,N是它与x轴的两个交点,D,C分别为它的最高点和最低点,点F(0,1)是线段MD的中点,三角形MDC的面积为$\frac{2π}{3}$.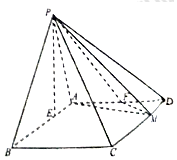 在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.
在四棱锥P-ABCD中,底面ABCD为平行四边形,AB=3,$AD=2\sqrt{2}$,∠ABC=45°,P点在底面ABCD内的射影E在线段AB上,且PE=2,BE=2EA,F为AD的中点,M在线段CD上,且CM=λCD.