题目内容
16．
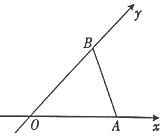用斜二测画法画一个水平放置的平面图形的直观图为如图所示的等腰三角形，其中OA=OB=1，则原平面图形的面积为（ ）| A． | 1 | B． | $\sqrt{2}$ | C． | $\frac{3}{2}$ | D． | 2 |
分析 根据斜二测画法规则，把直观图还原成原平面图，再求该平面图形的面积．
解答 解：根据斜二测画法规则，把直观图还原成原平面图形如图所示，
则该平面图形是直角三角形，
它的面积为S=$\frac{1}{2}$O′A′•O′B′=$\frac{1}{2}$×1×2=1．
故选：A．
点评 本题考查了斜二测画直观图的应用问题，也考查了求平面图形面积的应用问题，是基础题．
练习册系列答案
相关题目
6．复数$\frac{5i}{{2+{i^9}}}$的共轭复数所对应的点位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
7．已知二项分布ξ～B（4，$\frac{1}{2}$），则该分布列的方差Dξ值为（ ）
| A． | 4 | B． | 3 | C． | 1 | D． | 2 |
11．已知$a={log_{\frac{1}{5}}}\frac{2}{5}$，$b={3^{\frac{3}{5}}}$，$c={4^{\frac{1}{5}}}$，则a，b，c的大小关系是（ ）
| A． | a＜c＜b | B． | c＜b＜a | C． | a＜b＜c | D． | b＜a＜c |
1．《九章算术》是我国古代数学名著，也是古代东方数学的代表作．书中有如下问题：“今有勾五步，股十二步，问勾中容方几何？”其意思为：“已知直角三角形两直角边长分别为5步和12步，问其内接正方形边长为多少步？”现若向此三角形内投豆子，则落在其内接正方形内的概率是（ ）
| A． | $\frac{60}{289}$ | B． | $\frac{90}{289}$ | C． | $\frac{120}{289}$ | D． | $\frac{240}{289}$ |
已知空间几何体CBEADF如图所示，底面AEFD为矩形，平面BEFC⊥平面AEFD，∠CFE=∠BEF=90°，其中AE+BE=AD=2，DF+CF=4．