题目内容
二次函数y=ax2,(a>0)的图象开口向 ,对称轴是 ,顶点坐标是 ,图象有最 点,x 时,y随x的增大而增大,x 时,y随x的增大而减小.
考点:二次函数的性质
专题:函数的性质及应用
分析:根据已知中二次函数y=ax2,a>0,可判断图象的开口方向,代入对称轴方程和顶点坐标公式,可得对称轴方程和顶点坐标,进而根据函数的图象形状,判断y随x的增大的变化趋势.
解答:
解:∵a>0,
∴二次函数y=ax2的图象开口向上;
对称轴为直线x=0,即y轴;
顶点坐标为(0,0);
图象有最低点;
当x>0(x≥0)时,y随x的增大而增大,
当x<0(x≤0)时,y随x的增大而减小.
故答案为:上,y轴,(0,0),低,>0,<0
∴二次函数y=ax2的图象开口向上;
对称轴为直线x=0,即y轴;
顶点坐标为(0,0);
图象有最低点;
当x>0(x≥0)时,y随x的增大而增大,
当x<0(x≤0)时,y随x的增大而减小.
故答案为:上,y轴,(0,0),低,>0,<0
点评:本题考查的知识点是二次函数的图象和性质,是对二次函数基本知识点的考查,难度不大,属于基础题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
在抛物线y=-x2上,当y<0时,x的取值范围应为( )
| A、x>0 | B、x<0 |
| C、x≠0 | D、x≥0 |
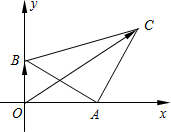 如图,等腰Rt△ABC直角边的两端点A,B分别在x轴、y轴的正半轴上移动,若|AB|=2,则
如图,等腰Rt△ABC直角边的两端点A,B分别在x轴、y轴的正半轴上移动,若|AB|=2,则