题目内容

在抛物线y=-x2上，当y＜0时，x的取值范围应为（　　）
A、x＞0B、x＜0
C、x≠0D、x≥0
考点：二次函数的性质
专题：函数的性质及应用
分析：根据抛物线y=-x2的图象和性质，说明其自变量的取值范围即可．
解答： 解：抛物线y=-x2的开口向下，顶点为（0，0），
∴只有当x=0时，y=0，不存在x值，使y＞0
∴当x≠0时，y＜0，
故选C．
点评：本题考查了二次函数的性质，解题的关键是了解二次函数y=-x2的性质．
练习册系列答案
相关题目
二次函数y=ax2，（a＞0）的图象开口向
 
，对称轴是
 
，顶点坐标是
 
，图象有最
 
点，x
 
时，y随x的增大而增大，x
 
时，y随x的增大而减小．
若（cosφ+x）5的展开式中x3的系数为2，则cos2φ=
 
．
设y=f（x）是定义在R上的函数，则“x≠1”是“f（x）≠f（1）”成立的（　　）
A、充分不必要条件
B、必要不充分条件
C、充分必要条件
D、既不充分也不必要条件
如果抛物线y=x2+6x+c的顶点在x轴上，那么c的值为（　　）
A、0B、6C、3D、9
若某程序框图如图所示，则该程序运行后输出的值是（　　）
 
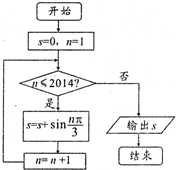
A、-
3
B、-
3
2
C、
3
D、
3
2
执行如图所示的程序框图，则输出的n为（　　）
A、3B、6C、5D、4
已知x，y满足约束条件
x-y≥-5
x+y≥0
x≤3
，则z=2x+4y的最小值是（　　）
A、-6B、5C、38D、-10
已知二次函数f（x）=ax2+bx（a、b∈R）满足：①f（4+x）=f（4-x）②对一切x∈R，都有f（x）≤x，
（1）求f（x）；
（2）设集合A={x∈R|f（x）＞0}，B={x∈R|2x2-3（1+a）x+6a＜0}，若A∩B=B，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网