题目内容
2.已知函数f(x)=|2x-a|+a.(1)若不等式f(x)≤6的解集为{x|-2≤x≤3},求实数a的值;
(2)在(1)的条件下,若存在实数t,使$f({\frac{t}{2}})$≤m-f(-t)成立,求实数m的取值范围.
分析 (1)原不等式可化为|2x-a|≤6-a,解得a-3≤x≤3.再根据不等式f(x)≤6的解集为[-2,3],可得a-3=-2,从而求得a的值.
(2)由题意可得|t-1|+|2t+1|+2≤m,根据函数y=|t-1|+|2t+1|+2=$\left\{\begin{array}{l}{2-3t,t≤-\frac{1}{2}}\\{t+4,-\frac{1}{2}<t<1}\\{3t+2,t≥1}\end{array}\right.$,得y的最小值,从而求得m的范围.
解答 解:(1)原不等式可化为|2x-a|≤6-a,
∴$\left\{\begin{array}{l}{6-a≥0}\\{a-6≤2x-a≤6-a}\end{array}\right.$,
解得a-3≤x≤3.
再根据不等式f(x)≤6的解集为[-2,3],可得a-3=-2,
∴a=1.
(2)∵f(x)=|2x-1|+1,f($\frac{t}{2}$)≤m-f(-t),
∴|t-1|+1≤m-(|-2t-1|+1),
∴|t-1|+|2t+1|+2≤m,
∵y=|t-1|+|2t+1|+2=$\left\{\begin{array}{l}{2-3t,t≤-\frac{1}{2}}\\{t+4,-\frac{1}{2}<t<1}\\{3t+2,t≥1}\end{array}\right.$,
∴ymin=3.5,
∴m≥3.5,即m的范围是[3.5,+∞).
点评 本题主要考查绝对值不等式的解法,带有绝对值的函数,体现了转化的数学思想,属于中档题.

练习册系列答案
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
20.3、已知函数$f(x)=\left\{\begin{array}{l}1-{2^x},x≤0\\{x^2},x>0\end{array}\right.$,则f[f(-1)]=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
17.下列结论正确的是( )
| A. | 命题“如果p2+q2=2,则p+q≤2”的否命题是“如果p+q>2,则p2+q2≠2” | |
| B. | 命题p:?x∈[0,1],ex≥1,命题q:?x∈R,x2+x+1<0,则p∨q为假 | |
| C. | “若am2<bm2,则a<b”的逆命题为真命题 | |
| D. | 若${(\sqrt{x}-\frac{1}{{2\root{3}{x}}})^n}$的展开式中第四项为常数项,则n=5 |
12.三个数0.76,60.7,log0.76的大小关系为( )
| A. | ${log_{0.7}}6<{0.7^6}<{6^{0.7}}$ | B. | 0.76<60.7<log0.76 | ||
| C. | ${log_{0.7}}6<{6^{0.7}}<{0.7^6}$ | D. | ${0.7^6}<{log_{0.7}}6<{6^{0.7}}$ |
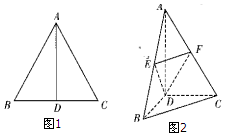 如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.
如图,边长为2的等边三角形ABC中,D为BC的中点,将△ABC沿AD翻折成直二面角B-AD-C,点E,F分别是AB,AC的中点.