题目内容
20.3、已知函数$f(x)=\left\{\begin{array}{l}1-{2^x},x≤0\\{x^2},x>0\end{array}\right.$,则f[f(-1)]=( )| A. | 2 | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 先求出f(-1)=1-2-1=$\frac{1}{2}$,从f[f(-1)]=f($\frac{1}{2}$),由此能求出结果.
解答 解:∵函数$f(x)=\left\{\begin{array}{l}1-{2^x},x≤0\\{x^2},x>0\end{array}\right.$,
∴f(-1)=1-2-1=$\frac{1}{2}$,
f[f(-1)]=f($\frac{1}{2}$)=$(\frac{1}{2})^{2}$=$\frac{1}{4}$.
故选:C.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
11.用数学归纳法证明1+a+a2+…+an+1=$\frac{{1-{a^{n+2}}}}{1-a}({a≠0,1,n∈{N^*}})$,在验证n=1成立时,计算左边所得的项是( )
| A. | 1 | B. | 1+a | C. | a2 | D. | 1+a+a2 |
5.在△ABC中,若b2+c2=a2-bc,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
1.已知数列{an}为等比数列,其中a5,a9为方程x2+2016x+9=0的二根,则a7的值( )
| A. | -3 | B. | 3 | C. | ±3 | D. | 9 |
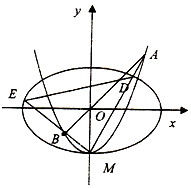 如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的短轴长,C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于点D、E.
如图,椭圆C1:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,x轴被曲线C2:y=x2-b截得的线段长等于C1的短轴长,C2与y轴的交点为M,过坐标原点O的直线l与C2相交于点A、B,直线MA,MB分别与C1相交于点D、E.