题目内容
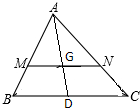 如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN,分别交AB,AC于M,N两点,若
如图,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN,分别交AB,AC于M,N两点,若| AM |
| AB |
| AN |
| AC |
| 1 |
| x |
| 1 |
| y |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:根据图形得
=
-
=(
-x)
+
,
=
-
=y
-
(
+
)=-
+(y-
)
,利用共线向量的条件得出(
-x)(y-
)+
=0,
化简即可得出
+
=4=定值.
| MG |
| AG |
| AM |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| GN |
| AN |
| AG |
| AC |
| 1 |
| 4 |
| AB |
| AC |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
化简即可得出
| 1 |
| x |
| 1 |
| y |
解答:
解: 根据题意得出,
根据题意得出,
△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN,分别交AB,AC于M,N两点,若
=x
,
=y
.
∴
=
=
(
+
),
∴
=
-
=(
-x)
+
,
=
-
=y
-
(
+
)=-
+(y-
)
,
∵
∥
,
∴(
-x)(y-
)+
=0,
即
(x+y)-xy=0,
∴
+
=4=定值.
 根据题意得出,
根据题意得出,△ABC中,D为BC的中点,G为AD的中点,过点G任作一直线MN,分别交AB,AC于M,N两点,若
| AM |
| AB |
| AN |
| AC |
∴
| AG |
| 1 |
| 2 |
| AD |
| 1 |
| 4 |
| AB |
| AC |
∴
| MG |
| AG |
| AM |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
| GN |
| AN |
| AG |
| AC |
| 1 |
| 4 |
| AB |
| AC |
| 1 |
| 4 |
| AB |
| 1 |
| 4 |
| AC |
∵
| MG |
| GN |
∴(
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 16 |
即
| 1 |
| 4 |
∴
| 1 |
| x |
| 1 |
| y |
点评:本题考查的知识点是向量的线性运算性质及几何意义,向量的共线定理,及三角形的重心,其中根据
与
共线,根据共线向量基本定理知,进而得到x,y的关系式,是解答本题的关键.
| MG |
| NG |

练习册系列答案
相关题目
 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,D是AB中点,(直三棱柱,指侧棱垂直于底面的棱柱).
在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,D是AB中点,(直三棱柱,指侧棱垂直于底面的棱柱).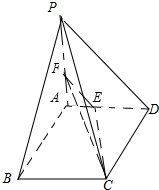

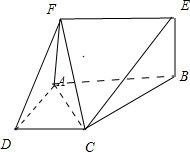 已知平面ABEF⊥平面ABCD、长方形ABEF,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4
已知平面ABEF⊥平面ABCD、长方形ABEF,∠DAB=90°,AB∥CD,AD=AF=CD=2,AB=4