题目内容
在平面直角坐标系中,△ABC的两个顶点A,B的坐标分别是(-
,0),(
,0),点G是△ABC的重心,y轴上一点M满足GM∥AB,且|MC|=|MB|.
(Ⅰ)求△ABC的顶点C的轨迹E的方程;
(Ⅱ)不过点A的直线l与轨迹E交于不同的两点P,Q.若以PQ为直径的圆过点A时,试判断直线l是否过定点?若过,请求出定点坐标,不过,说明理由.
| 2 |
| 2 |
(Ⅰ)求△ABC的顶点C的轨迹E的方程;
(Ⅱ)不过点A的直线l与轨迹E交于不同的两点P,Q.若以PQ为直径的圆过点A时,试判断直线l是否过定点?若过,请求出定点坐标,不过,说明理由.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:(Ⅰ)设点C坐标为(x,y),推出△ABC的重心故G点坐标为(
,
),由|MC|=|MB|,求解△ABC的顶点C的轨迹E的方程.
(Ⅱ)设直线l:y=kx+b与
+
=1的两交点为P(x1,y1),Q(x2,y2),联立:
利用韦达定理,结合
•
=0,然后求解b与k的关系.求出直线系方程,然后求出直线过定点坐标.
| x |
| 3 |
| y |
| 3 |
(Ⅱ)设直线l:y=kx+b与
| x2 |
| 2 |
| y2 |
| 6 |
|
| AP |
| AQ |
解答:
解:(Ⅰ)设点C坐标为(x,y)
因为G为△ABC的重心故G点坐标为(
,
),∴M(0,
)…(2分)
由|MC|=|MB|得∴x2+(
y)2=2+(
)2,…(3分)
即
+
=1(y≠0)
∴△ABC的顶点C的轨迹E的方程是
+
=1(y≠0)…(5分)
(Ⅱ)设直线l:y=kx+b与
+
=1的两交点为P(x1,y1),Q(x2,y2)
联立:
消去y得:(k2+3)x2+2kbx+b2-6=0…(7分)
∴△=4k2b2-4(k2+3)(b2-6)=12(2k2-b2+6)>0,
且x1+x2=-
,x1x2=
.…(8分)
若以PQ为直径的圆过点A时,则有
•
=0.…(9分)
∴(x1+
)(x2+
)+y1y2=0,既有(x1+
)(x2+
)+(kx1+b)(kx2+b)=0,
故(k2+1)x1x2+(kb+
)(x1+x2)+b2+2=0,
代入整理得:2b2-
kb-2k2=0…(11分)∴b=-
k或b=
k.…(12分)
(1)当b=-
k.时,y=kx+b=k(x-
)直线过定点(
,0),
且代入△>0成立; …(13分)
(2)当b=
k时,y=kx+b=k(x+
),直线过点(-
,0),不合题意,舍去.
综上知:直线过定点(
,0)…14
因为G为△ABC的重心故G点坐标为(
| x |
| 3 |
| y |
| 3 |
| y |
| 3 |
由|MC|=|MB|得∴x2+(
| 2 |
| 3 |
| y |
| 3 |
即
| x2 |
| 2 |
| y2 |
| 6 |
∴△ABC的顶点C的轨迹E的方程是
| x2 |
| 2 |
| y2 |
| 6 |
(Ⅱ)设直线l:y=kx+b与
| x2 |
| 2 |
| y2 |
| 6 |
联立:
|
∴△=4k2b2-4(k2+3)(b2-6)=12(2k2-b2+6)>0,
且x1+x2=-
| 2kb |
| k2+3 |
| b2-6 |
| k2+3 |
若以PQ为直径的圆过点A时,则有
| AP |
| AQ |
∴(x1+
| 2 |
| 2 |
| 2 |
| 2 |
故(k2+1)x1x2+(kb+
| 2 |
代入整理得:2b2-
| 2 |
| ||
| 2 |
| 2 |
(1)当b=-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
且代入△>0成立; …(13分)
(2)当b=
| 2 |
| 2 |
| 2 |
综上知:直线过定点(
| ||
| 2 |
点评:本题考查直线与圆锥曲线的综合应用,轨迹方程的求法,直线系的应用,考查分析问题解决问题的能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
f(x)=ex-x-2在下列那个区间必有零点( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
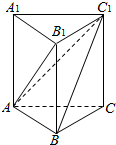 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形A1ACC1是边长为2的正方形,AB=BC=
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,四边形A1ACC1是边长为2的正方形,AB=BC=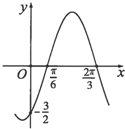 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<