题目内容
设集合A={x|x2<4},B={x|1<
}.
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
| 4 |
| x+3 |
(1)求集合A∩B;
(2)若不等式2x2+ax+b<0的解集为B,求a,b的值.
考点:交集及其运算
专题:集合
分析:(1)求出A与B中不等式的解集确定出A与B,求出两集合的交集即可;
(2)根据已知不等式的解集为B,得到-3和1为2x2+ax+b=0的两根,利用根与系数的关系求出a与b的值即可.
(2)根据已知不等式的解集为B,得到-3和1为2x2+ax+b=0的两根,利用根与系数的关系求出a与b的值即可.
解答:
解:(1)∵A={x|x2<4}={x|-2<x<2},B={x|1<
}={x|
<0}={x|-3<x<1},
∴A∩B={x|-2<x<1};
(2)∵不等式2x2+ax+b<0的解集为B={x|-3<x<1},
∴-3和1为2x2+ax+b=0的两根,
可得
,
解得:a=4,b=-6.
| 4 |
| x+3 |
| x-1 |
| x+3 |
∴A∩B={x|-2<x<1};
(2)∵不等式2x2+ax+b<0的解集为B={x|-3<x<1},
∴-3和1为2x2+ax+b=0的两根,
可得
|
解得:a=4,b=-6.
点评:此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知m,n∈R,则“lnm<lnn”是“em<en”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、不充分不必要条件 |
下列不等式中,正确的是( )
A、tan
| ||||
B、sin
| ||||
C、sin
| ||||
D、cos
|
到两定点F1(-3,0)、F2(3,0)的距离之差的绝对值等于6的点M的轨迹( )
| A、两条射线 | B、线段 |
| C、双曲线 | D、椭圆 |
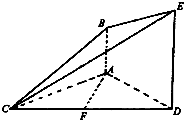 如图,已知DE⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.
如图,已知DE⊥平面ACD,DE∥AB,△ACD是正三角形,AD=DE=2AB=2,且F是CD的中点.