题目内容
已知
=(
,3),
=(cos(θ+
),2),若θ为锐角,且
∥
,则cosθ的值为 .
| m |
| 9 |
| 10 |
| n |
| π |
| 6 |
| m |
| n |
考点:平面向量共线(平行)的坐标表示
专题:平面向量及应用
分析:根据向量平行的坐标公式,结合三角函数的关系即可得到结论.
解答:
解:∵
∥
,
∴3cos(θ+
)-
×2=0,
即cos(θ+
)=
,
∵θ为锐角,
∴sin(θ+
)=
,
则cosθ=cos(θ+
-
)=cos(θ+
)cos
+sin(θ+
)sin
=
×
+
×
=
,
故答案为:
| m |
| n |
∴3cos(θ+
| π |
| 6 |
| 9 |
| 10 |
即cos(θ+
| π |
| 6 |
| 3 |
| 5 |
∵θ为锐角,
∴sin(θ+
| π |
| 6 |
| 4 |
| 5 |
则cosθ=cos(θ+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| 1 |
| 2 |
4+3
| ||
| 10 |
故答案为:
4+3
| ||
| 10 |
点评:本题主要考查两角和的余弦公式的应用,利用向量平行的坐标公式是解决本题的关键,考查学生的计算能力.

练习册系列答案
相关题目
下列函数中,既是偶函数,又在(0,+∞)上单调递减的是( )
A、y=
| ||
| B、y=x2-4 | ||
| C、y=cosx | ||
D、y=log
|
为了有效管理学生迟到问题,某校专对各班迟到现象制定了相应的等级标准,其中D级标准为“连续10天,每天迟到不超过7人”根据过去10天1、2、3、4班的迟到数据,一定符合D级标准的是( )
| A、1班:总体平均值为3,中位数为4 |
| B、2班:总体平均值为1,总体方差大于0 |
| C、3班:中位数为2,众数为3 |
| D、4班:总体平均值为2,总体方差为3 |
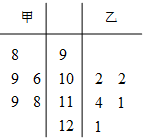 在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如图茎叶图所示:
在数学趣味知识培训活动中,甲、乙两名学生的5次培训成绩如图茎叶图所示: