题目内容
△ABC中,∠C=90°,M是BC的中点,若sin∠BAC=
,则sin∠BAM= .
| ||
| 3 |
考点:正弦定理
专题:解三角形
分析:先根据题意分别设出BC,AB,则CM,AC,sinB,AM可求,最后利用正弦定理可求得sin∠BAM.
解答:
解:依题意sin∠BAC=
=
,
设BC=
t,则AB=3t,
CM=
BC=
,AC=
t=
t,sinB=
=
∴AM=
t=
t,
∵
=
,
∴sin∠BAM=
•BM=
×
•
×
•t=
.
故答案为:
.
| BC |
| AB |
| ||
| 3 |
设BC=
| 3 |
CM=
| 1 |
| 2 |
| ||
| 2 |
| 9-3 |
| 6 |
| AC |
| AB |
| ||
| 3 |
∴AM=
6+
|
3
| ||
| 2 |
∵
| BM |
| sin∠BAM |
| AM |
| sin∠B |
∴sin∠BAM=
| sin∠B |
| AM |
| ||
| 3 |
| 2 | ||
3
|
| 1 |
| t |
| ||
| 2 |
| ||
| 9 |
故答案为:
| ||
| 9 |
点评:本题主要考查了正弦定理的应用.在直角三角形中应充分利用好勾股定理求得相应的边长.

练习册系列答案
相关题目
运行如图的程序图,则输出s的结果是( )


A、
| ||
B、
| ||
C、
| ||
D、
|
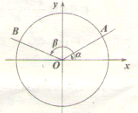 如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y=
如图所示,锐角α和钝角β的始边与x轴的非负半轴重合,终边分别与单位圆交于A、B两点,角α的终边与射线y= 如图是某中学甲、乙两名学生2014年篮球比赛每场比赛得分的茎叶图,则甲、乙两名学生得分的中位数之和是
如图是某中学甲、乙两名学生2014年篮球比赛每场比赛得分的茎叶图,则甲、乙两名学生得分的中位数之和是