题目内容
已知函数f(x)=ax+
.
(Ⅰ)从区间(-2,2)内任取一个实数a,设事件A={函数y=f(x)-2在区间(0,+∞)上有两个不同的零点},求事件A发生的概率;
(Ⅱ)若连续掷两次骰子(骰子六个面上标注的点数分别为1,2,3,4,5,6)得到的点数分别为a和b,记事件B={f(x)>b2在x∈(0,+∞)恒成立},求事件B发生的概率.
| 4 |
| x |
(Ⅰ)从区间(-2,2)内任取一个实数a,设事件A={函数y=f(x)-2在区间(0,+∞)上有两个不同的零点},求事件A发生的概率;
(Ⅱ)若连续掷两次骰子(骰子六个面上标注的点数分别为1,2,3,4,5,6)得到的点数分别为a和b,记事件B={f(x)>b2在x∈(0,+∞)恒成立},求事件B发生的概率.
考点:古典概型及其概率计算公式
专题:概率与统计
分析:(Ⅰ)首先求出参数的取值范围,再利用概率公式计算即可.
(Ⅱ)先求出f(x)的最小值,然后讨论a的取值,找到满足条件的基本事件,根据概率公式计算即可.
(Ⅱ)先求出f(x)的最小值,然后讨论a的取值,找到满足条件的基本事件,根据概率公式计算即可.
解答:
解:(Ⅰ)∵函数y=f(x)-2在区间(0,+∞)上有两个不同的零点,
∴f(x)-2=0,即ax2-2x+4=0有两个不同的正根x1和x2
∴
⇒0<a<
∴P(A)=
=
(Ⅱ)由已知:a>0,x>0,所以f(x)≥2
,即f(x)≥4
∴f(x)min=4
,
∵f(x)>b2在x∈(0,+∞)恒成立
∴4
>b2…(*)
当a=1时,b=1适合(*);
当a=2,3,4,5时,b=1,2均适合(*);
当a=6时,b=1,2,3均适合(*);
满足(*)的基本事件个数为1+8+3=12.
而基本事件总数为6×6=36,
∴P(B)=
=
.
∴f(x)-2=0,即ax2-2x+4=0有两个不同的正根x1和x2
∴
|
| 1 |
| 4 |
∴P(A)=
| ||
| 4 |
| 1 |
| 16 |
(Ⅱ)由已知:a>0,x>0,所以f(x)≥2
ax•
|
| a |
∴f(x)min=4
| a |
∵f(x)>b2在x∈(0,+∞)恒成立
∴4
| a |
当a=1时,b=1适合(*);
当a=2,3,4,5时,b=1,2均适合(*);
当a=6时,b=1,2,3均适合(*);
满足(*)的基本事件个数为1+8+3=12.
而基本事件总数为6×6=36,
∴P(B)=
| 12 |
| 36 |
| 1 |
| 3 |
点评:本题主要考查了古典概型的概率问题以及函数的零点和最值问题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
已知复数z=2+i,
是z的共轭复数,则
对应的点位于( )
. |
| z |
| ||
| z |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
在(2
-
)5的二项展开式中,x的系数为( )
| x |
| 1 |
| x |
| A、-80 | B、-5 | C、10 | D、80 |
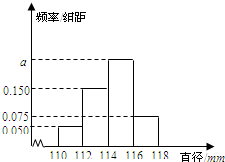 某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.
某工厂生产的产品A的直径均位于区间[110,118]内(单位:mm).若生产一件产品A的直径位于区间[110,112],[112,114],[114,116],[116,118]内该厂可获利分别为10,20,30,10(单位:元),现从该厂生产的产品A中随机100件测量它们的直径,得到如图所示的频率分布直方图.