题目内容
试做一个上端开口的圆柱形容器,它的净容积为V,壁厚为a(包括侧壁和底部),其中V和a均为常数.问容器内壁半径为多少时,所用的材料最少?
考点:导数在最大值、最小值问题中的应用
专题:导数的概念及应用
分析:设容器内壁的半径为x(x>0),容器的高为h,构造函数f(x)=π(x+a)2a+π(x+a)2h-V.利用导数确定函数的最值,从而求出容器内壁半径为
时,所用的材料最少.
| 3 |
| ||
解答:
解:设容器内壁的半径为x(x>0),容器的高为h,
则h=
.
∴所用材料f(x)=底部所用材料=侧壁所用材料
=π(x+a)2a+π(x+a)2h-V.
∴f′(x)=2πa(x+a)-2aV(
+
)
=
(x3-
)(x2+
x+(
)2)
令f′(x)=0得,x=
.
∴函数在x=
处取得最小值.
∴容器内壁半径为
时,所用的材料最少.
则h=
| V |
| πx2 |
∴所用材料f(x)=底部所用材料=侧壁所用材料
=π(x+a)2a+π(x+a)2h-V.
∴f′(x)=2πa(x+a)-2aV(
| 1 |
| x2 |
| 1 |
| a2 |
=
| 2aπ(x+a) |
| x3 |
| 3 |
| ||
| 3 |
| ||
| 3 |
| ||
令f′(x)=0得,x=
| 3 |
| ||
∴函数在x=
| 3 |
| ||
∴容器内壁半径为
| 3 |
| ||
点评:本题考查利用导数求函数最值,构造函数解决实际问题等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)为奇函数,x>0时,f(x)=sin2x+cosx,则x<0时,f(x)为( )
| A、sin2x-cosx |
| B、sin2x+cosx |
| C、cosx-sin2x |
| D、-sin2x-cosx |
已知θ为实数,若复数z=sin2θ-1+i(
cosθ-1)是纯虚数,则z的虚部为( )
| 2 |
| A、2 | B、0 | C、-2 | D、-2i |
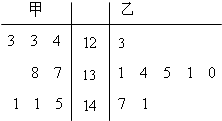 为了解某校高一学生的中考数学成绩,分别从甲乙两班随机各抽取8名学生的中考数学成绩,获得如图所示的茎叶图.
为了解某校高一学生的中考数学成绩,分别从甲乙两班随机各抽取8名学生的中考数学成绩,获得如图所示的茎叶图.