题目内容
求由曲线y=x3在点（3，27）处的切线，曲线y=x3和x轴围成的区域的面积．
考点：定积分在求面积中的应用
专题：综合题,导数的综合应用
分析：利用导数的几何意义，求出切线方程，确定被积函数与被积区间，求出原函数，即可得到结论．
解答：
解：求导函数，可得y′=3x2，
当x=3时，y′=27，∴曲线y=x3在点（3，27）处的切线方程为y-27=27（x-3），即y=27x-54．
∴所求区域的面积为S=
(x3-27x+54)dx=（
x4-
x2+54x）
=
．
当x=3时，y′=27，∴曲线y=x3在点（3，27）处的切线方程为y-27=27（x-3），即y=27x-54．
∴所求区域的面积为S=
| ∫ | 3 0 |
| 1 |
| 4 |
| 27 |
| 2 |
| | | 3 0 |
| 27 |
| 4 |
点评：本题考查导数的几何意义，考查切线方程，考查学生的计算能力，确定曲线交点的坐标，确定被积区间及被积函数是解题的关键．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目
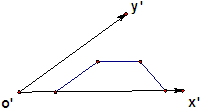一个水平放置的平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形，则该平面图形的面积等于（ ）A、
| ||||||
B、1+
| ||||||
C、1+
| ||||||
D、2+
|
某程序框图如图所示，则该程序运行后输出的值为（ ）
| A、23 | B、47 | C、95 | D、191 |